Construction of triangle

Construction of triangle

We have already learnt in previous class how to construct triangles when sides and angles are given.

In this section, let us construct a triangle when the following are given :

(i) the base, vertical angle and the median on the base

(ii) the base, vertical angle and the altitude on the base

(iii) the base, vertical angle and the point on the base where the bisector of the vertical angle meets the base.

First, we consider the following construction,

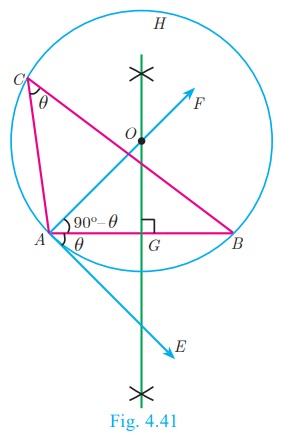
Construction of a segment of a circle on a given line segment containing an angle θ

Construction

Step 1: Draw a line segment 

Step 2: At A, take ∠BAE = θ Draw AE. 

Step 3: Draw, AF ┴ AE .

Step 4: Draw the perpendicular bisector of AB meeting AF at O. 

Step 5: With O as centre and OA as radius draw a circle ABH.

Step 6: Take any point C on the circle, By the alternate segments theorem, the major arc ACB is the required segment of the circle containing the angle θ.

Note

If C ₁ , C₂,... are points on the circle, then all the triangles ΔBAC ₁ , ΔBAC₂,... are with same base and the same vertical angle.

Construction of a triangle when its base, the vertical angle and the median from the vertex of the base are given.

Example 4.17

Construct a ΔPQR in which PQ = 8 cm, ∠R = 60° and the median RG from R to PQ is 5.8 cm. Find the length of the altitude from R to PQ. 

Solution

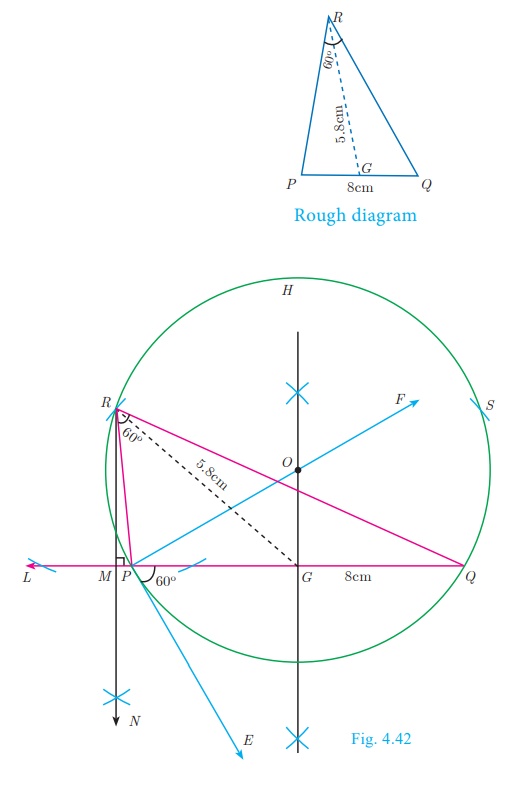
Construction

Step 1: Draw a line segment PQ = 8cm.

Step 2: At P, draw PE such that ∠QPE = 60°.

Step3: At P, draw PF such that ∠EPF = 90°.

Step 4: Draw the perpendicular bisector to PQ, which intersects PF at O and PQ at G.

Step 5: With O as centre and OP as radius draw a circle.

Step 6: From G mark arcs of radius 5.8 cm on the circle. Mark them as R and S .

Step 7 : Join PR and RQ. Then ΔPQR is the required triangle.

Step 8 : From R draw a line RN perpendicular to LQ. LQ meets RN at M 

Step 9: The length of the altitude is RM = 3.5 cm.  

Note

We can get another ΔPQS for the given measurements.

Construct a triangle when its base, the vertical angle and the altitude from the vertex to the base are given.

Example 4.18

Construct a triangle ΔPQR such that QR = 5 cm, ∠P = 30° and the altitude from P to QR is of length 4.2 cm.

Construction

Step 1 : Draw a line segment QR = 5 cm.

Step 2 : At Q draw QE such that ∠RQE = 30°.

Step 3 : At Q draw QF such that ∠EQF = 90°.

Step 4 : Draw the perpendicular bisector XY to QR which intersects QF at O and QR at G.

Step 5 : With O as centre and OQ as radius draw a circle.

Step 6: From G mark an arc in the line XY at M, such that GM = 4. 2 cm.

Step 7: Draw AB through M which is parallel to QR.

Step 8: AB meets the circle at P and S.

Step 9: Join QP and RP. Then  ΔPQR is the required triangle.

Note

ΔSQR  is  another required triangle for the given measurements.

Construct of a triangle when its base, the vertical angle and the point on the base where the bisector of the vertical angle meets the base

Example 4.19

Draw a triangle ABC of base BC = 8 cm,  ∠A = 60° and the bisector of ∠A meets BC at D such that BD = 6 cm.

Solution

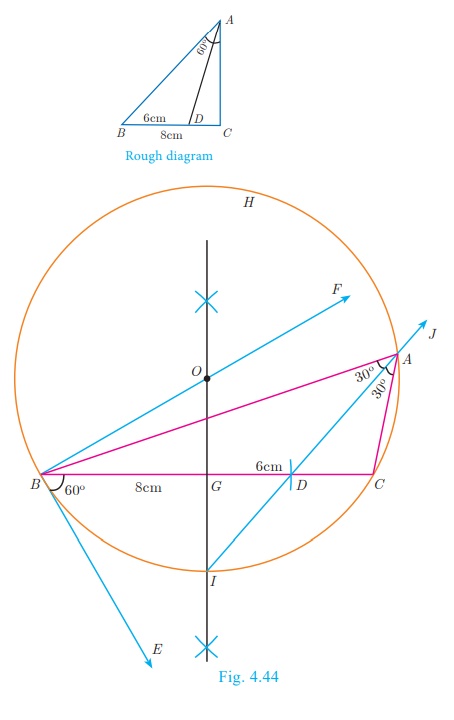
Construction

Step 1 : Draw a line segment BC= 8 cm.

Step 2 : At B, draw BE such that ∠CBE = 60°

Step 3 : At B, draw BF such that ∠EBF = 90° .

Step 4 : Draw the perpendicular bisector to BC, which intersects BF at O and BC at G.

Step 5 : With O as centre and OB as radius draw a circle.

Step 6 : From B, mark an arc of 6cm on BC at D.

Step 7 : The perpendicular bisector intersects the circle at I. Joint ID.

Step 8 : ID produced meets the circle at A. Now join AB and AC. Then ΔABC is the required triangle.