Pythagoras Theorem

Pythagoras Theorem

Among all existing theorems in mathematics, Pythagoras theorem is considered to be the most important because it has maximum number of proofs. There are more than 350 ways of proving Pythagoras theorem through different methods. Each of these proofs was discovered by eminent mathematicians, scholars, engineers and math enthusiasts, including one by the 20^th American president James Garfield. The book titled “The Pythagorean Proposition” written by Elisha Scott Loomis, published by the National Council of Teaching of Mathematics (NCTM) in America contains 367 proofs of Pythagoras Theorem.

Three numbers (a , b,c) are said to form Pythagorean Triplet, if they form sides of a right triangle. Thus (a , b,c) is a Pythagorean Triplet if and only if c² = a² +b².

Now we are in a position to study this most famous and important theorem not only in Geometry but in whole of mathematics.

Note

·           In a right angled triangle, the side opposite to 90° (the right angle) is called the hypotenuse.

·           The other two sides are called legs of the right angled triangle.

·           The hypotenuse will be the longest side of the triangle.

Theorem 5 : Pythagoras Theorem

Statement

In a right angle triangle, the square on the hypotenuse is equal to the sum of the squares on the other two sides.

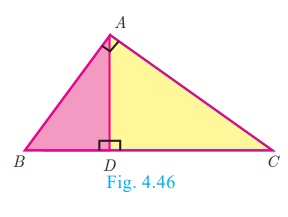
Proof

Given : In ΔABC, ∠A = 90°

To prove: AB ² + AC ² = BC ²

Construction : Draw AD ┴ BC

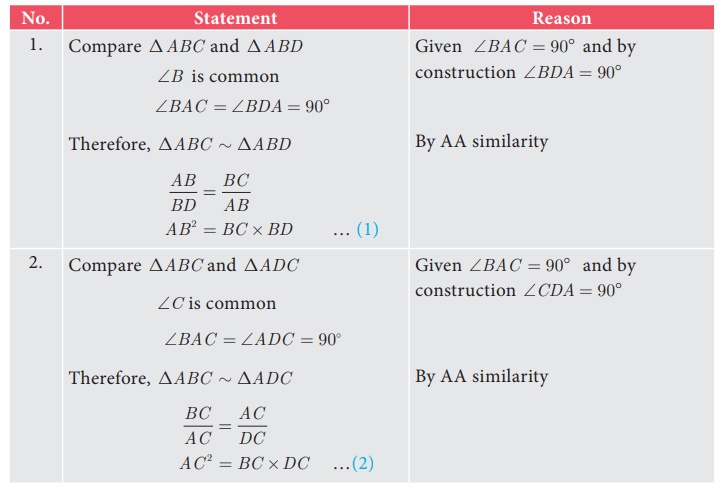
Adding (1) and (2) we get

AB ²+ AC ²= BC × BD + BC ×DC

= BC (BD + DC) = BC ×BC

AB ² + AC ²= BC ²    

Hence the theorem is proved.

Converse of Pythagoras Theorem

Statement

If the square of the longest side of a triangle is equal to sums of squares of other two sides, then the triangle is a right angle triangle.

Example 4.20

An insect 8 m away initially from the foot of a lamp post which is 6 m tall, crawls towards it moving through a distance. If its distance from the top of the lamp post is equal to the distance it has moved, how far is the insect away from the foot of the lamp post?

Solution

Distance between the insect and the foot of the lamp post BD = 8 m

The height of the lamp post, AB = 6 m

After moving a distance of x m, let the insect be at C

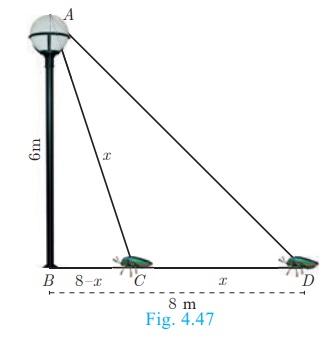
Let, AC = CD = x . Then BC = BD −CD = 8 − x

In ΔABC , ∠B = 90°

AC ² = AB² + BC ² gives x ² = 6² + (8 − x)²

x² = 36 + 64 − 16x + x²

16x = 100  then x = 6. 25

Then, BC = 8 − x = 8 − 6.25 = 1. 75 m

Therefore the insect is 1.75 m away from the foot of the lamp post.

Example 4.21

P and Q are the mid-points of the sides CA and CB respectively of a ΔABC, right angled at C. Prove that 4(AQ² + BP² ) = 5AB² .

Solution

Since, ΔAQC is a right triangle at C, AQ² = AC ²+QC ^{2                ………}(1)

Also, ΔBPC is a right triangle at C,   BP² = BC²+CP^{2                       …….}(2)

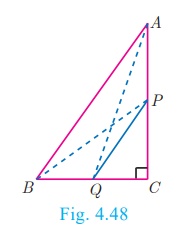
From (1) and (2), AQ² + BP²  = AC ² + QC ² + BC ² +CP²

4(AQ²  + BP² ) = 4AC ²  + 4QC ²  + 4BC ²  + 4CP²

= 4AC ²  + (2QC)²  + 4BC ²  + (2CP)²

= 4AC ² + BC ² + 4BC ² + AC ²   (Since P and Q are mid points)

= 5(AC ²  + BC ² )

4(AQ²  + BP² ) = 5AB² (By Pythagoras Theorem)

Example 4.22

What length of ladder is needed to reach a height of 7 ft along the wall when the base of the ladder is 4 ft from the wall? Round off your answer to the next tenth place.

Solution

Let x be the length of the ladder. BC= 4 ft, AC= 7 ft.

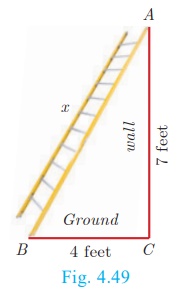
By Pythagoras theorem we have, AB²  = AC² + BC²

x²  = 7 ² + 4²  gives x²  = 49 + 16

x²  = 65 . Hence, x =  √65

The number √65 is between 8 and 8.1.

8²  = 64 < 65 < 65.61 = 8.1²

Therefore, the length of the ladder is approximately 8.1 ft.

Example 4.23

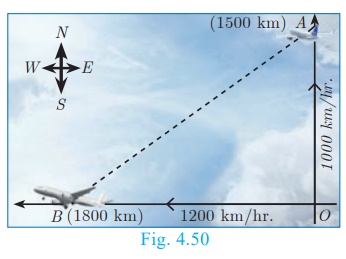
An Aeroplane leaves an airport and flies due north at a speed of 1000 km/hr. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km/hr. How far apart will be the two planes after 1½ hours?

Solution 

Let the first aeroplane starts from O and goes upto A towards north, (Distance=Speed×time) 

where OA= ( 1000 × 3/2 )km =1500 km

Let the second aeroplane starts from O at the same time and goes upto B towards west,

where OB= ( 1200 × 3/2 )km = 1800 km

The required distance to be found is BA.

In right angled tirangle AOB, AB²  = OA² +OB²

AB²   = (1500)² + (1800)² = 100² (15²+18²)

= 100² × 549 = 100² × 9 × 61

AB = 100 × 3 × √61

= 300√(61) kms.