Testing the consistency of non homogeneous linear equations (two and three variables) by rank method

Testing the consistency of non homogeneous linear equations (two and three variables) by rank method.

Consider the equations A X= B in ‘n’ unknowns.

(i) If ρ ([A, B] ) = ρ ( A) , then the equations are consistent.

(ii) If ρ[([A, B] ) = ρ ( A )= n , then the equations are consistent and have unique solution.

(iii) If ρ ([ A, B] ) = ρ ( A ) < n , then the equations are consistent and have infinitely many solutions.

(iv) If ρ ([A, B ]) ≠ ρ ( A) then the equations are inconsistent and has no solution.

Example 1.9

Show that the equations x + y = 5, 2x + y = 8 are consistent and solve them.

Solution:

The matrix equation corresponding to the given system is

AX=B

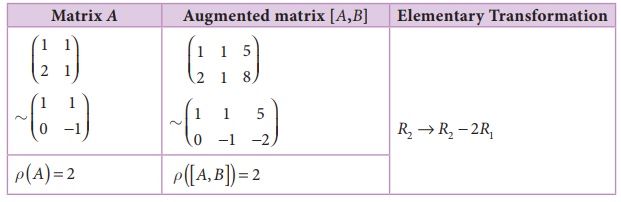
Number of non-zero rows is 2.  

ρ (A )= ρ ([ A, B]) = 2 = Number of unknowns.  

The given system is consistent and has unique solution. 

Now, the given system is transformed into

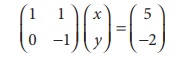
x + y = 5

y = 2

∴ (1) ⇒ x + 2 = 5

x = 3

Solution is x = 3, y = 2

Example 1.10

Show that the equations 2x + y = 5, 4x + 2 y = 10 are consistent and solve them.

Solution:

The matrix equation corresponding to the system is

ρ ( A ) = ρ ([ A, B]) = 1 < number of unknowns

∴ The given system is consistent and has infinitely many solutions.

Now, the given system is transformed into the matrix equation.

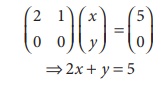
Let us take y = k, k ∈R

⇒ 2x + k = 5

x = 1/2 ( 5 − k)

x = 1/2 ( 5 − k) , y = k for all k ∈R

Thus by giving different values for k, we get different solution. Hence the system has infinite number of solutions.

Example 1.11

Show that the equations 3x − 2 y = 6, 6x − 4 y = 10 are inconsistent.

Solution:

The matrix equation corresponding to the given system is

∴The given system is inconsistent and has no solution.

Example 1.12

Show that the equations 2x + y + z = 5, x + y + z = 4, x − y + 2z = 1 are consistent and hence solve them.

Solution:

The matrix equation corresponding to the given system is

Obviously the last equivalent matrix is in the echelon form. It has three non-zero rows.

ρ( A ) = ρ( [A, B] )= 3 = Number of unknowns .

The given system is consistent and has unique solution.

To find the solution, let us rewrite the above echelon form into the matrix form.

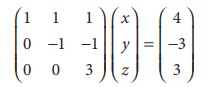
x + y + z = 4 (1)

 y + z = 3 (2)

3z = 3 (3)

(3)⇒ z = 1

(2)⇒ y = 3 − z = 2

(1) ⇒ x = 4 − y − z

x=1

∴ x = 1, y = 2, z = 1

Example 1.13

Show that the equations x + y + z = 6, x + 2 y + 3z = 14, x + 4 y + 7z = 30 are consistent and solve them.

Solution:

The matrix equation corresponding to the given system is

Obviously the last equivalent matrix is in the echelon form. It has two non-zero rows.

∴ ρ ( [A, B] ) = 2, ρ ( A) = 2

ρ ( A ) = ρ ( [A, B] ) = 2 < Number of unknowns.

The given system is consistent and has infinitely many solutions.

The given system is equivalent to the matrix equation,

x + y + z = 6  (1)

y + 2z = 8 (2)

(2)⇒ y = 8 − 2z,

(1)⇒ x = 6 − y − z = 6 − (8 − 2 z) − z = z – 2

Let us take z = k, k ∈R , we get x = k − 2, y = 8 − 2k , Thus by giving different values for k we get different solutions. Hence the given system has infinitely many solutions.

Example 1.14

Show that the equations x − 4 y + 7z = 14, 3x + 8 y − 2z = 13, 7x − 8 y + 26z = 5 are inconsistent.

Solution:

The matrix equation corresponding to the given system is

The last equivalent matrix is in the echelon form. [A, B] has 3 non-zero rows and [A] has 2 non-zero rows.

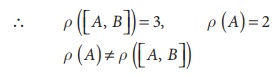
The system is inconsistent and has no solution.

Example 1.15

Find k, if the equations x + 2 y − 3z = −2, 3x − y − 2z = 1, 2x + 3y − 5z = k are consistent.

Solution:

The matrix equation corresponding to the given system is

For the equations to be consistent, ρ ( [A, B] ) = ρ ( A)= 2

∴21 + 7k = 0

7k = −21 .

k = −3

Example 1.16

Find k, if the equations x + y + z = 7, x + 2 y + 3z = 18, y + kz = 6 are inconsistent.

Solution:

The matrix equation corresponding to the given system is

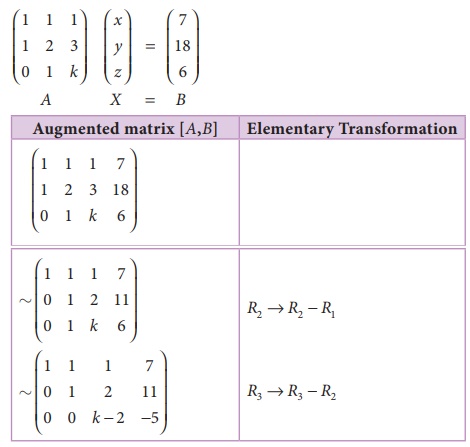
For the equations to be inconsistent

ρ ( [A, B] ) ≠ ρ ( A)

It is possible if k − 2 = 0 .

K=2

Example 1.17

Investigate for what values of ‘a’ and ‘b’ the following system of equations

x + y + z = 6, x + 2 y + 3z = 10, x + 2 y + az = b have 

(i) no solution  (ii) a unique solution (iii) an infinite number of solutions.

Solution:

The matrix equation corresponding to the given system is

Case (i) For no solution:

The system possesses no solution only when ρ ( A )≠ ρ ([ A, B]) which is possible only when a − 3 = 0 and b − 10 ≠ 0

Hence for a = 3, b ≠ 10 , the system possesses no solution.

Case (ii) For a unique solution:

The system possesses a unique solution only when ρ ( A ) = ρ ([ A, B]) = number of unknowns.

i.e when ρ ( A ) = ρ ([ A, B]) = 3

Which is possible only when a − 3 ≠ 0 and b may be any real number as we can observe .

Hence for a ≠ 3 and b ∈R , the system possesses a unique solution.

Case (iii) For an infinite number of solutions:

The system possesses an infinite number of solutions only when

ρ ( A )= ρ ([ A, B]) < number of unknowns

i,e when ρ ( A)= ρ ([ A, B])= 2 < 3 ( number of unknowns) which is possible only when a − 3 = 0, b − 10 = 0

Hence for a = 3, b =10, the system possesses infinite number of solutions.

Example 1.18

The total number of units produced (P) is a linear function of amount of over times in labour (in hours) (l), amount of additional machine time (m) and fixed finishing time (a)

i.e, P = a + bl + cm

From the data given below, find the values of constants a, b and c

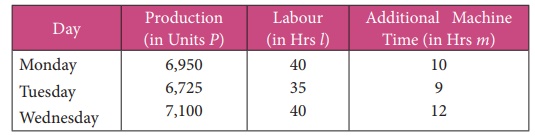
Estimate the production when overtime in labour is 50 hrs and additional machine time is 15 hrs.

Solution:

We have, P = a + bl + cm

Putting above values we have

6,950 = a + 40b + 10c

6,725 = a + 35b + 9c

7,100 = a + 40b + 12c

The Matrix equation corresponding to the given system is

∴ The given system is equivalent to the matrix equation

∴ The production equation is P = 5000 + 30l + 75m

 P_{at l = 50, m=15}         = 5000 + 30(50) + 75(15)

=7625 units.

∴The production = 7,625 units.