Chapter: 12th Business Maths and Statistics : Chapter 1 : Applications of Matrices and Determinants
Rank of a Matrix: Solved Example Problems
Example 1.1
Find the rank of the matrix 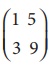
Solution:
Let A= 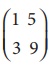
Order of A is 2 û 2 ãÇ ü(A)ãÊ 2
Consider the second order minor
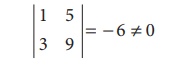
There is a minor of order 2, which is not zero. ãÇü (A) = 2
Example 1.2
Find the rank of the matrix 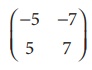
Solution:
Let A= 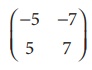
Order of A is 2 û 2 ãÇü(A)ãÊ 2
Consider the second order minor
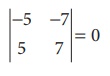
Since the second order minor vanishes, ü(A) ã 2
Consider a first order minor |ã5| ã 0
There is a minor of order 1, which is not zero
ãÇ ü (A) = 1
Example 1.3
Find the rank of the matrix 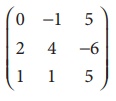
Solution:
Let A= 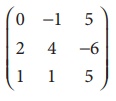
Order Of A is 3x3
ãÇ ü (A) ãÊ 3
Consider the third order minor 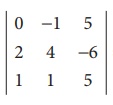 = 6 ã 0
= 6 ã 0
There is a minor of order 3, which is not zero
ãÇü (A) = 3.
Example 1.4
Find the rank of the matrix 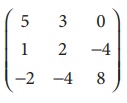
Solution:
Let A= 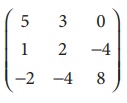
Order Of A is 3x3
ãÇ ü (A) ãÊ 3
Consider the third order minor 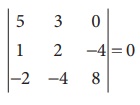
Since the third order minor vanishes, therefore ü(A) ã 3
Consider a second order minor 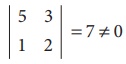
There is a minor of order 2, which is not zero.
ãÇ ü(A) = 2.
Example 1.5
Find the rank of the matrix 
Solution:
Let A = 
Order of A is 3 û 4
ãÇ ü(A)ãÊ 3.
Consider the third order minors

Since all third order minors vanishes, ü(A) ã 3.
Now, let us consider the second order minors,
Consider one of the second order minors 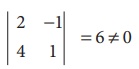
There is a minor of order 2 which is not zero.
ãÇü (A) = 2.
Echelon form and finding the rank of the matrix (upto the order of 3û4) : Solved Example Problems
Example 1.6
Find the rank of the matrix A= 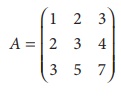
Solution :
The order of A is 3 û 3.
ãÇ ü(A) ãÊ 3.
Let us transform the matrix A to an echelon form by using elementary transformations.

The number of non zero rows is 2
ãÇRank of A is 2.
ü (A) = 2.
Note
A row having atleast one non -zero element is called as non-zero row.
Example 1.7
Find the rank of the matrix A= 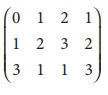
Solution:
The order of A is 3 û 4.
ãÇ ü (A)ãÊ3.
Let us transform the matrix A to an echelon form
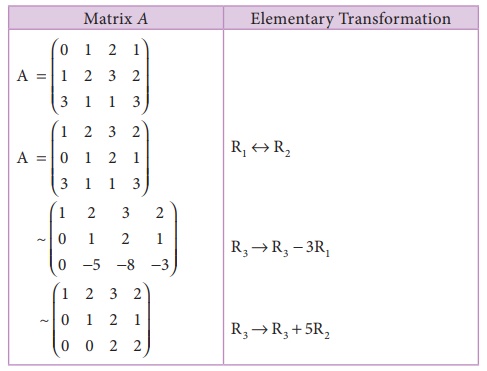
The number of non zero rows is 3. ãÇ ü(A) =3.
Example 1.8
Find the rank of the matrix A= 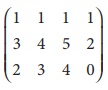
Solution:
The order of A is 3 û 4.
ãÇ ü(A) ãÊ 3.
Let us transform the matrix A to an echelon form
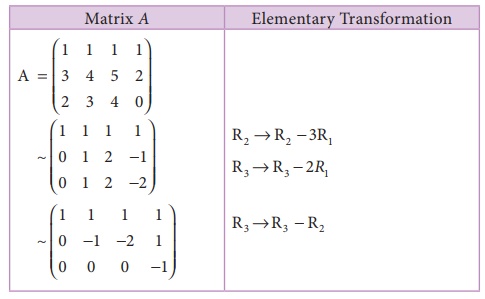
The number of non zero rows is 3.
ãÇ ü (A) =3.
Testing the consistency of non homogeneous linear equations (two and three variables) by rank method : Solved Example Problems
Example 1.9
Show that the equations x + y = 5, 2x + y = 8 are consistent and solve them.
Solution:
The matrix equation corresponding to the given system is

AX=B
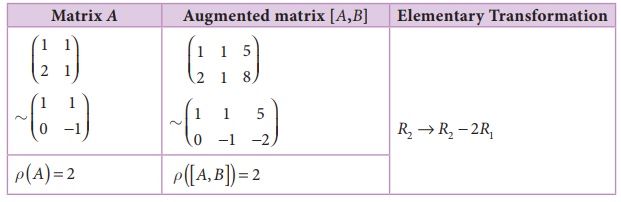
Number of non-zero rows is 2.
ü (A )= ü ([ A, B]) = 2 = Number of unknowns.
The given system is consistent and has unique solution.
Now, the given system is transformed into
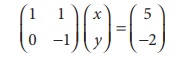
x + y = 5
y = 2
ãÇ (1) ã x + 2 = 5
x = 3
Solution is x = 3, y = 2
Example 1.10
Show that the equations 2x + y = 5, 4x + 2 y = 10 are consistent and solve them.
Solution:
The matrix equation corresponding to the system is

ü ( A ) = ü ([ A, B]) = 1 < number of unknowns
ãÇ The given system is consistent and has infinitely many solutions.
Now, the given system is transformed into the matrix equation.
Let us take y = k, k ãR
ã 2x + k = 5
x = 1/2 ( 5 ã k)
x = 1/2 ( 5 ã k) , y = k for all k ãR
Thus by giving different values for k, we get different solution. Hence the system has infinite number of solutions.
Example 1.11
Show that the equations 3x ã 2 y = 6, 6x ã 4 y = 10 are inconsistent.
Solution:
The matrix equation corresponding to the given system is

ãÇThe given system is inconsistent and has no solution.
Example 1.12
Show that the equations 2x + y + z = 5, x + y + z = 4, x ã y + 2z = 1 are consistent and hence solve them.
Solution:
The matrix equation corresponding to the given system is

Obviously the last equivalent matrix is in the echelon form. It has three non-zero rows.
ü( A ) = ü( [A, B] )= 3 = Number of unknowns .
The given system is consistent and has unique solution.
To find the solution, let us rewrite the above echelon form into the matrix form.
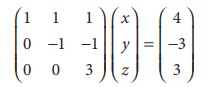
x + y + z = 4 (1)
y + z = 3 (2)
3z = 3 (3)
(3)ã z = 1
(2)ã y = 3 ã z = 2
(1) ã x = 4 ã y ã z
x=1
ãÇ x = 1, y = 2, z = 1
Example 1.13
Show that the equations x + y + z = 6, x + 2 y + 3z = 14, x + 4 y + 7z = 30 are consistent and solve them.
Solution:
The matrix equation corresponding to the given system is

Obviously the last equivalent matrix is in the echelon form. It has two non-zero rows.
ãÇ ü ( [A, B] ) = 2, ü ( A) = 2
ü ( A ) = ü ( [A, B] ) = 2 < Number of unknowns.
The given system is consistent and has infinitely many solutions.
The given system is equivalent to the matrix equation,

x + y + z = 6 (1)
y + 2z = 8 (2)
(2)ã y = 8 ã 2z,
(1)ã x = 6 ã y ã z = 6 ã (8 ã 2 z) ã z = z ã 2
Let us take z = k, k ãR , we get x = k ã 2, y = 8 ã 2k , Thus by giving different values for k we get different solutions. Hence the given system has infinitely many solutions.
Example 1.14
Show that the equations x ã 4 y + 7z = 14, 3x + 8 y ã 2z = 13, 7x ã 8 y + 26z = 5 are inconsistent.
Solution:
The matrix equation corresponding to the given system is

The last equivalent matrix is in the echelon form. [A, B] has 3 non-zero rows and [A] has 2 non-zero rows.
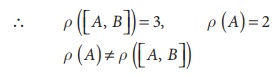
The system is inconsistent and has no solution.
Example 1.15
Find k, if the equations x + 2 y ã 3z = ã2, 3x ã y ã 2z = 1, 2x + 3y ã 5z = k are consistent.
Solution:
The matrix equation corresponding to the given system is

For the equations to be consistent, ü ( [A, B] ) = ü ( A)= 2
ãÇ21 + 7k = 0
7k = ã21 .
k = ã3
Example 1.16
Find k, if the equations x + y + z = 7, x + 2 y + 3z = 18, y + kz = 6 are inconsistent.
Solution:
The matrix equation corresponding to the given system is
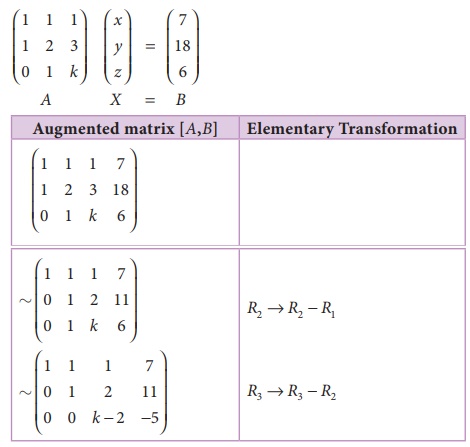
For the equations to be inconsistent
ü ( [A, B] ) ã ü ( A)
It is possible if k ã 2 = 0 .
K=2
Example 1.17
Investigate for what values of ãaã and ãbã the following system of equations
x + y + z = 6, x + 2 y + 3z = 10, x + 2 y + az = b have
(i) no solution (ii) a unique solution (iii) an infinite number of solutions.
Solution:
The matrix equation corresponding to the given system is

Case (i) For no solution:
The system possesses no solution only when ü ( A )ã ü ([ A, B]) which is possible only when a ã 3 = 0 and b ã 10 ã 0
Hence for a = 3, b ã 10 , the system possesses no solution.
Case (ii) For a unique solution:
The system possesses a unique solution only when ü ( A ) = ü ([ A, B]) = number of unknowns.
i.e when ü ( A ) = ü ([ A, B]) = 3
Which is possible only when a ã 3 ã 0 and b may be any real number as we can observe .
Hence for a ã 3 and b ãR , the system possesses a unique solution.
Case (iii) For an infinite number of solutions:
The system possesses an infinite number of solutions only when
ü ( A )= ü ([ A, B]) < number of unknowns
i,e when ü ( A)= ü ([ A, B])= 2 < 3 ( number of unknowns) which is possible only when a ã 3 = 0, b ã 10 = 0
Hence for a = 3, b =10, the system possesses infinite number of solutions.
Example 1.18
The total number of units produced (P) is a linear function of amount of over times in labour (in hours) (l), amount of additional machine time (m) and fixed finishing time (a)
i.e, P = a + bl + cm
From the data given below, find the values of constants a, b and c
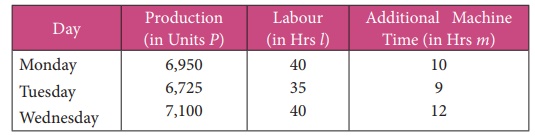
Estimate the production when overtime in labour is 50 hrs and additional machine time is 15 hrs.
Solution:
We have, P = a + bl + cm
Putting above values we have
6,950 = a + 40b + 10c
6,725 = a + 35b + 9c
7,100 = a + 40b + 12c
The Matrix equation corresponding to the given system is

ãÇ The given system is equivalent to the matrix equation

ãÇ The production equation is P = 5000 + 30l + 75m
Pat l = 50, m=15 = 5000 + 30(50) + 75(15)
=7625 units.
ãÇThe production = 7,625 units.
Related Topics