Rank of a Matrix: Concept

Rank of a Matrix

Matrices are one of the most commonly used tools in many fields such as Economics, Commerce and Industry.

We have already studied the basic properties of matrices. In this chapter we will study about the elementary transformations to develop new methods for various applications of matrices.

Concept

With each matrix, we can associate a non-negative integer called its rank.

Definition 1.1

The rank of a matrix A is the order of the largest non-zero minor of A and is denoted by ρ(A)

In other words, A positive integer ‘r’ is said to be the rank of a non- zero matrix A, if

(i) there is atleast one minor of A of order ‘r’ which is not zero and

(ii) every minor of A of order greater than ‘r’ is zero.

Note

(i)   ρ(A)≥ 0

(ii) If A is a matrix of order m × n , then ρ(A)≤ minimum of {m,n}

(iii)The rank of a zero matrix is ‘0’

(iv) The rank of a non- singular matrix of order n × n is ‘n’

Example 1.1

Find the rank of the matrix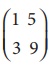 

Solution:

Let A=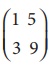 

Order of A is 2 × 2 ∴          ρ(A)≤ 2

Consider the second order minor

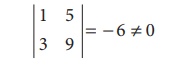
There is a minor of order 2, which is not zero. ∴ρ (A) = 2

Example 1.2

Find the rank of the matrix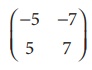 

Solution:

Let A=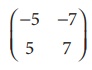 

Order of A is 2 × 2 ∴ρ(A)≤ 2

Consider the second order minor

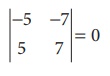
Since the second order minor vanishes, ρ(A) ≠ 2

Consider a first order minor |−5| ≠ 0

There is a minor of order 1, which is not zero

∴ ρ (A) = 1

Example 1.3

Find the rank of the matrix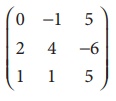 

Solution:

Let A=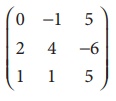 

Order Of A is 3x3

∴ ρ (A) ≤ 3

Consider the third order minor 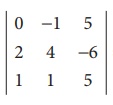 = 6 ≠ 0

There is a minor of order 3, which is not zero

∴ρ (A) = 3.

Example 1.4

Find the rank of the matrix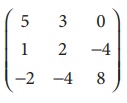 

Solution:

Let A=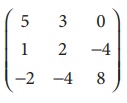 

Order Of A is 3x3

∴ ρ (A) ≤ 3

Consider the third order minor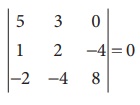 

Since the third order minor vanishes, therefore ρ(A) ≠ 3

Consider a second order minor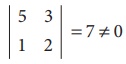 

There is a minor of order 2, which is not zero.

∴ ρ(A) = 2.

Example 1.5

Find the rank of the matrix 

Solution:

Let A = 

Order of A is 3 × 4

∴ ρ(A)≤ 3.

Consider the third order minors

Since all third order minors vanishes, ρ(A) ≠ 3.

Now, let us consider the second order minors,

Consider one of the second order minors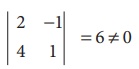 

There is a minor of order 2 which is not zero.

∴ρ (A) = 2.