Problem Questions with Answer, Solution - Exercise 1.1 : Rank of a Matrix | 12th Business Maths and Statistics : Chapter 1 : Applications of Matrices and Determinants
Chapter: 12th Business Maths and Statistics : Chapter 1 : Applications of Matrices and Determinants
Exercise 1.1 : Rank of a Matrix
Exercise 1.1
1. Find the rank of each of the following matrices
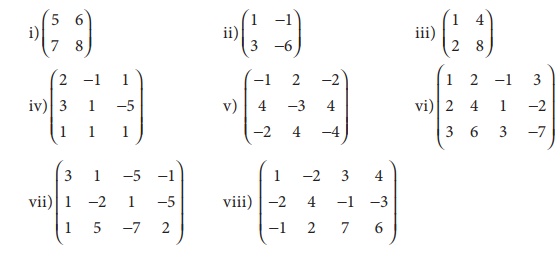





2. If A = 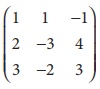 and B =
and B = 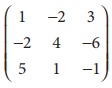 , then find the rank of AB and the rank of BA.
, then find the rank of AB and the rank of BA.


3. Solve the following system of equations by rank method
x + y + z = 9, 2x + 5y + 7z = 52, 2x ã y ã z = 0


4. Show that the equations 5x + 3y + 7z = 4, 3x + 26 y + 2z = 9, 7x + 2 y + 10z = 5 are consistent and solve them by rank method.


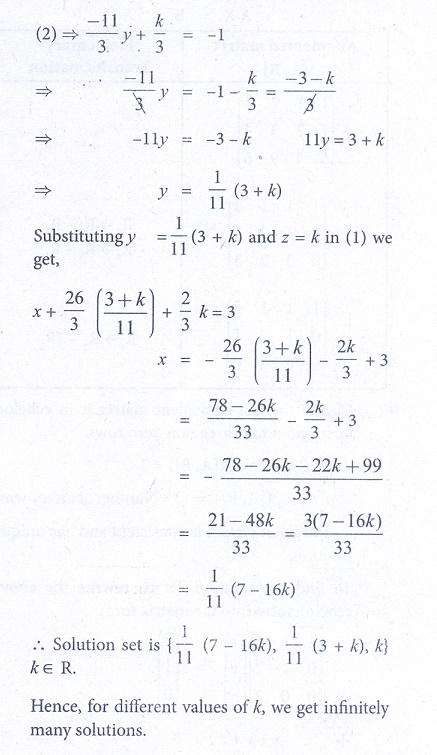
5. Show that the following system of equations have unique solution:
x + y + z = 3, x + 2 y + 3z = 4, x + 4 y + 9z = 6 by rank method.


6. For what values of the parameter ö£ , will the following equations fail to have unique solution: 3x ã y + ö£ z = 1, 2x + y + z = 2, x + 2 y ã ö£ z = ã1 by rank method.

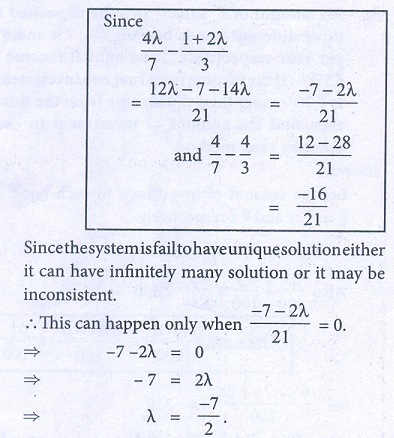
7. The price of three commodities X,Y and Z are x,y and z respectively Mr.Anand purchases 6 units of Z and sells 2 units of X and 3 units of Y. Mr.Amar purchases a unit of Y and sells 3 units of X and 2units of Z. Mr.Amit purchases a unit of X and sells 3 units of Y and a unit of Z. In the process they earn ã¿5,000/-, ã¿2,000/- and ã¿5,500/- respectively Find the prices per unit of three commodities by rank method.



8. An amount of ã¿5,000/- is to be deposited in three different bonds bearing 6%, 7% and 8% per year respectively. Total annual income is ã¿358/-. If the income from first two investments is ã¿70/- more than the income from the third, then find the amount of investment in each bond by rank method.


Answers:
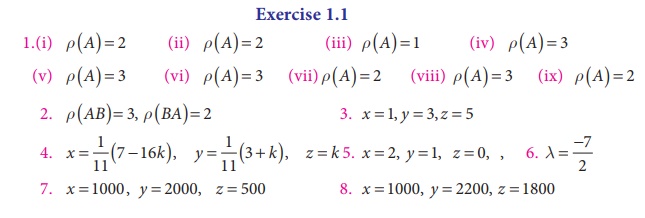
Related Topics