Cramer’s Rule - Non Homogeneous linear equations upto three variables: Solved Example Problems

Cramer’s Rule (Non Homogeneous linear equations upto three variables): Solved Example Problems

Example 1.19

Solve the equations 2x + 3y = 7, 3x + 5y = 9 by Cramer’s rule.

Solution:

The equations are

2x + 3y = 7

3x + 5y = 9

Here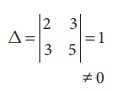 

∴ we can apply Cramer’s Rule

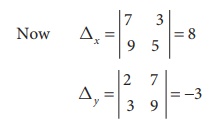
∴ By Cramer’s rule

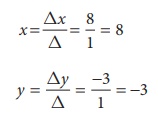
∴    Solution is      x = 8, y = −3

Example 1.20

The following table represents the number of shares of two companies A and B during the month of January and February and it also gives the amount in rupees invested by Ravi during these two months for the purchase of shares of two companies. Find the the price per share of A and Bpurchased during both the months

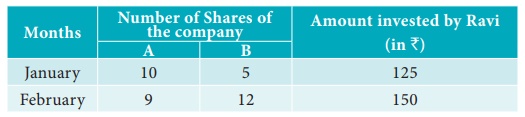
Solution:

Let the price of one share of A be x

Let the price of one share of B be y

∴ By given data, we get the following equations

10x + 5y = 125

9x + 12 y = 150

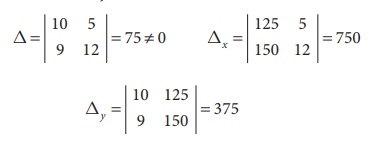
∴ By Cramer’s rule

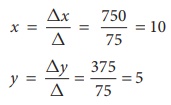
The price of the share A is â‚¹10 and the price of the share B is â‚¹5.

Example 1.21

The total cost of 11 pencils and 3 erasers is ₹ 64 and the total cost of 8 pencils and 3 erasers is ₹49. Find the cost of each pencil and each eraser by Cramer’s rule.

Solution:

Let ‘x’ be the cost of a pencil

Let ‘y’ be the cost of an eraser

∴ By given data, we get the following equations

11x + 3y =64

8x+3y=49

∴ The cost of a pencil is ₹ 5 and the cost of an eraser is ₹ 3.

Example 1.22

Solve by Cramer’s rule x + y + z = 4, 2x âˆ’ y + 3z = 1, 3x + 2 y âˆ’ z = 1

Solution:

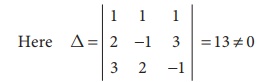
∴ We can apply Cramer’s Rule and the system is consistent and it has unique solution.

The solution is     ( x , y, z) = ( −1,3, 2)

Example 1.23

The price of 3 Business Mathematics books, 2 Accountancy books and one Commerce book is ₹840. The price of 2 Business Mathematics books, one Accountancy book and one Commerce book is ₹570. The price of one Business Mathematics book, one Accountancy book and 2 Commerce books is ₹630. Find the cost of each book by using Cramer’s rule.

Solution:

Let ‘x’ be the cost of a Business Mathematics book

Let ‘y’ be the cost of a Accountancy book.

Let ‘z’ be the cost of a Commerce book.

∴ 3x + 2 y + z = 840

2x + y + z = 570

x + y + 2z = 630

∴ The cost of a Business Mathematics book is ₹120,

 the cost of a Accountancy book is ₹150 and

the cost of a Commerce book is ₹180.

Example 1.24

An automobile company uses three types of Steel S1, S 2 and S3 for providing three different types of Cars C1, C2 and C3. Steel requirement R (in tonnes) for each type of car and total available steel of all the three types are summarized in the following table.

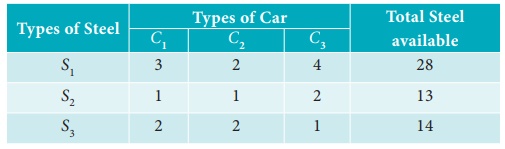
Determine the number of Cars of each type which can be produced by Cramer’s rule.

Solution:

Let ‘x’ be the number of cars of type C1

Let ‘y’ be the number of cars of type C2

Let ‘z’ be the number of cars of type C3

3x + 2 y + 4z = 28

x + y + 2z = 13

2x + 2 y + z = 14

∴ The number of cars of each type which can be produced are 2, 3 and 4.