System of Resistors

SYSTEM OF RESISTORS

So far, you have learnt how the resistance of a conductor affects the current through a circuit. You have also studied the case of the simple electric circuit containing a single resistor. Now in practice, you may encounter a complicated circuit, which uses a combination of many resistors. This combination of resistors is known as ‘system of resistors’ or ‘grouping of resistors’. Resistors can be connected in various combinations. The two basic methods of joining resistors together are:

a) Resistors connected in series, and b) Resistors connected in parallel.

In the following sections, you shall compute the effective resistance when many resistors having different resistance values are connected in series and in parallel.

1. Resistors in series

A series circuit connects the components one after the other to form a ‘single loop’. A series circuit has only one loop through which current can pass. If the circuit is interrupted at any point in the loop, no current can pass through the circuit and hence no electric appliances connected in the circuit will work. Series circuits are commonly used in devices such as flashlights. Thus, if resistors are connected end to end, so that the same current passes through each of them, then they are said to be connected in series.

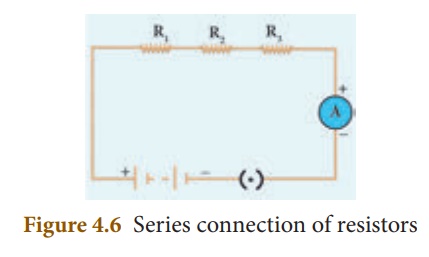
Let, three resistances R₁, R₂ and R₃ be connected in series (Figure 4.6). Let the current flowing through them be I. According to Ohm’s Law, the potential differences V₁, V₂ and V₃ across R₁, R₂ and R₃ respectively, are given by:

V₁ = I R₁ (4.7)

V₂ = I R₂ ( 4.8)

V₃ = I R₃ (4.9)

The sum of the potential differences across the ends of each resistor is given by:

V = V₁ + V₂ + V₃

Using equations (4.7), (4.8) and (4.9), we get

V = I R₁ + I R₂ + I R₃ (4.10)

The effective resistor is a single resistor, which can replace the resistors effectively, so as to allow the same current through the electric circuit. Let, the effective resistance of the series-combination of the resistors, be R_S. Then,

V = I R_S (4.11)

Combining equations (4.10) and (4.11), you get,

I R_S = I R₁ + I R₂ + I R₃

R_S = R₁ + R₂ + R₃ (4.12)

Thus, you can understand that when a number of resistors are connected in series, their equivalent resistance or effective resistance is equal to the sum of the individual resistances. When ‘n’ resistors of equal resistance R are connected in series, the equivalent resistance is ‘n R’.

i.e., R_S = n R

The equivalent resistance in a series combination is greater than the highest of the individual resistances.

Solved Problem

Three resistors of resistances 5 ohm, 3 ohm and 2 ohm are connected in series with 10 V battery. Calculate their effective resistance and the current flowing through the circuit.

Solution:

R₁ = 5 Ω, R₂ = 3 Ω, R₃ = 2 Ω, V = 10 V

Rs = R₁ + R₂ + R₃, Rs = 5 + 3 + 2 = 10, hence

Rs = 10 Ω

The current, I = V/Rs = 10/10 = 1 A

2. Resistances in Parallel

A parallel circuit has two or more loops through which current can pass. If the circuit is disconnected in one of the loops, the current can still pass through the other loop(s). The wiring in a house consists of parallel circuits.

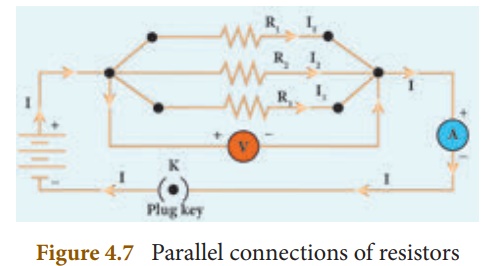
Consider that three resistors R₁, R₂ and R₃ are connected across two common points A and B. The potential difference across each resistance is the same and equal to the potential difference between A and B. This is measured using the voltmeter. The current I arriving at A divides into three branches I₁, I₂ and I₃ passing through R₁, R₂ and R₃ respectively.

According to the Ohm’s law, you have,

The total current through the circuit is given by

I = I₁ + I₂ + I₃

Using equations (4.13), (4.14) and (4.15), you get

Let the effective resistance of the parallel combination of resistors be R_P. Then,

Combining equations (4.16) and (4.17), you have

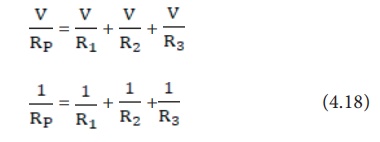
Thus, when a number of resistors are connected in parallel, the sum of the reciprocals of the individual resistances is equal to the reciprocal of the effective or equivalent resistance. When ‘n’ resistors of equal resistances R are connected in parallel, the equivalent resistance is R/n.

The equivalent resistance in a parallel combination is less than the lowest of the individual resistances.

3. Series Connection of Parallel Resistors

If you consider the connection of a set of parallel resistors that are connected in series, you get a series – parallel circuit. Let R₁ and R₂ be connected in parallel to give an effective resistance of R_P1. Similarly, let R₃ and R₄ be connected in parallel to give an effective resistance of R_P2. Then, both of these parallel segments are connected in series (Figure 4.8).

Using equation (4.18), you get

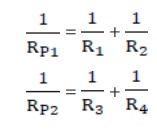
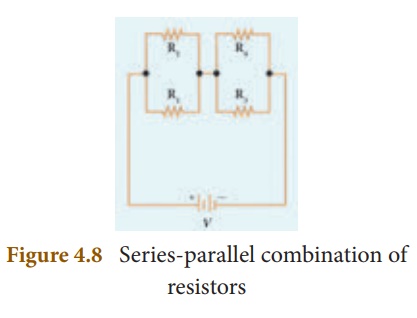
Finally, using equation (4.12), the net effective resistance is given by R_total = R_P1 + R_P2

4. Parallel Connection of Series Resistors

If you consider a connection of a set of series resistors connected in a parallel circuit, you get a parallel-series circuit. Let R1 and R2 be connected in series to give an effective resistance of RS1. Similarly, let R3 and R4 be connected in series to give an effective resistance of RS2. Then,both of these serial segments are connected in parallel (Figure 4.9).

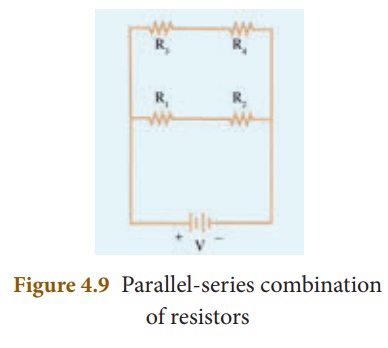
Using equation (4.12), you get

R_S1 = R₁ + R₂,

R_S2 = R₃ + R₄

Finally, using equation (4.18), the net effective resistance is given by

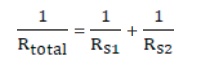
5. Comparison between series and parallel connections

The difference between series and parallel circuits may be summed as follows in Table 4.3