Synchronizing physical clocks

Synchronizing physical clocks

Two models of synchronization

1) External synchronization 

2) Internal synchronization

External synchronization: a computer‘s clock Ci is synchronized with an external authoritative time source S, so that:

|S(t) - Ci(t)| < D for i = 1, 2, …N over an interval, I of real time

The clocks Ci are accurate to within the bound D.

Internal synchronization: the clocks of a pair of computers are synchronized with one another so that:

| Ci(t) - Cj(t)| < D for i = 1, 2, … N over an interval, I of real time

The clocks Ci and Cj agree within the bound D.

Internally synchronized clocks are not necessarily externally synchronized, as they may drift collectively

if the set of processes P is synchronized externally within a bound D, it is also internally synchronized within bound 2D (worst case polarity)

Clock correctness

Correct clock: a hardware clock H is said to be correct if its drift rate is within a bound ρ > 0

(e.g. 10-6 secs/ sec)

This means that the error in measuring the interval between real times t and t’ is bounded:

(1 - ρ ) (t’ - t) ≤ H(t’) - H(t) ≤ (1 + ρ ) (t’ - t) (where t’>t) Which forbids jumps in time readings of hardware clocks

Clock monotonicity: weaker condition of correctness – t' > t ⇒ C(t’) > C(t) e.g. required by Unix make

A hardware clock that runs fast can achieve monotonicity by adjusting the values of α and β such that Ci(t)= αHi(t) + β

Faulty clock: a clock not keeping its correctness condition crash failure - a clock stops ticking

arbitrary failure - any other failure e.g. jumps in time; Y2K bug

Synchronization in a synchronous system

A synchronous distributed system is one in which the following bounds are defined

The time to execute each step of a process has known lower and upper bounds each message transmitted over a channel is received within a knownbounded time (min and max) each process has a local clock whose drift rate from real time has a known bound

Internal synchronization in a synchronous system

One process p1 sends its local time t to process p2 in a message m

p2 could set its clock to t + Ttrans where Ttrans is the time to transmit m

Ttrans is unknown but min ≤ Ttrans ≤ max

uncertainty u = max-min. Set clock to t + (max - min)/2 then skew ≤ u/2

Cristian‘s method for an asynchronous system

A time server S receives signals from a UTC source

Process p requests time in mr and receives t in mt from S

p sets its clock to t + Tround/2

Accuracy ± (Tround/2 - min) :

because the earliest time S puts t in message mt is min after p sent mr

the latest time was min before mt arrived at p

the time by S‘s clock when mt arrives is in the range [t+min, t + Tround - min]

the width of the range is Tround + 2min

The Berkeley algorithm

Problem with Cristian‘s algorithm

a single time server might fail, so they suggest the use of a group of synchronized servers

it does not deal with faulty servers

Berkeley algorithm (also 1989)

An algorithm for internal synchronization of a group of computers

A master polls to collect clock values from the others (slaves)

The master uses round trip times to estimate the slaves‘ clock values

It takes an average (eliminating any above some average round trip time or with faulty clocks)

It sends the required adjustment to the slaves (better than sending the time which depends on the round trip time)

Measurements

15 computers, clock synchronization 20-25 millisecs drift rate < 2x10-5

If master fails, can elect a new master to take over (not in bounded time)

Network Time Protocol (NTP)

A time service for the Internet - synchronizes clients to UTC Reliability from redundant paths, scalable, authenticates time sources Architecture

Primary servers are connected to UTC sources

Secondary servers are synchronized to primary servers

Synchronization subnet - lowest level servers in users‘ computers

strata: the hierarchy level

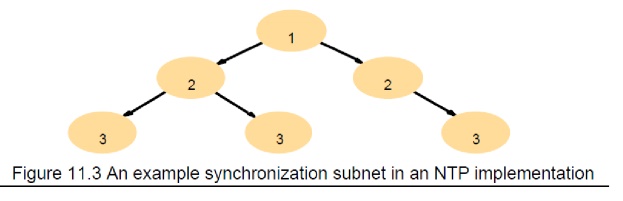
NTP - synchronization of servers

The synchronization subnet can reconfigure if failures occur

a primary that loses its UTC source can become a secondary

a secondary that loses its primary can use another primary

Modes of synchronization for NTP servers:

Multicast

A server within a high speed LAN multicasts time to others which set clocks assuming some delay (not very accurate)

Procedure call

A  server  accepts  requests  from  other  computers  (like

Cristian‘s algorithm)

Higher accuracy. Useful if no hardware multicast.

Messages exchanged between a pair of NTP peers

All modes use UDP

Each message bears timestamps of recent events:

Local times of Send and Receive of previous message

Local times of Send of current message

Recipient notes the time of receipt Ti ( we have Ti-3, Ti-2, Ti-1, Ti)

Estimations of clock offset and message delay

For each pair of messages between two servers, NTP estimates an offset oi (between the two clocks) and a delay di (total time for the two messages, which take t and t‘)

Ti-2 = Ti-3 + t + o and Ti = Ti-1 + t‘ - o

This gives us (by adding the equations) : di = t + t‘ = Ti-2 - Ti-3 + Ti - Ti-1

Also (by subtracting the equations)

= oi + (t‘ - t )/2 where oi = (Ti-2 - Ti-3 + Ti-1 - Ti )/2

Using the fact that t, t‘>0 it can be shown that

oi - di /2 ≤ o ≤ oi + di /2 .

Thus oi is an estimate of the offset and di is a measure of the accuracy

Data filtering

NTP servers filter pairs <oi, di>, estimating reliability from variation (dispersions), allowing them to select peers; and synchronization based on the lowest dispersion or min di ok

A relatively high filter dispersion represents relatively unreliable data

Accuracy of tens of milliseconds over Internet paths (1 ms on LANs)