Clocks, Events and Process States

CLOCKS, EVENTS AND PROCESS STATES

Each process executes on a single processor, and the processors do not share memory (Chapter 6 briefly considered the case of processes that share memory). Each process pi in has a state si that, in general, it transforms as it executes. The process’s state includes the values of all the variables within it. Its state may also include the values of any objects in its local operating system environment that it affects, such as files. We assume that processes cannot communicate with one another in any way except by sending messages through the network.

So, for example, if the processes operate robot arms connected to their respective nodes in the system, then they

are not allowed to communicate by shaking one another’s robot hands! As each process pi executes it takes a series of actions, each of which is either amessage send or receive operation, or an operation that transforms pi ’s state – one that

changes one or more of the values in si. In practice, we may choose to use a high-leveldescription of the actions, according to the application. For example, if the processes in are engaged in an eCommerce application, then the actions may be ones such as ‘client dispatched order message’ or ‘merchant server recorded transaction to log’.

We define an event to be the occurrence of a single action that a process carries out as it executes – a communication action or a state-transforming action. The sequence of events within a single process pi can be placed in a single, total ordering, which we denote by the relation i between the events.

That is, if and only if the event e occurs before e at pi . This ordering is well defined, whether or not the process is multithreaded,

since we have assumed that the process executes on a single processor. Now we can define the history of process pi to be the series of events that take place within it, ordered as we have described by the relation Clocks • We have seen how to order the events at a process, but not how to timestamp them – i.e., to assign to them a date and time of day. Computers each contain their own physical clocks. These clocks are electronic devices that count oscillations occurring in a crystal at a definite frequency, and typically divide this count and store the result in a counter register. Clock devices can be programmed to generate interrupts at regular intervals in order that, for example, timeslicing can be implemented; however, we shall not concern ourselves with this aspect of clock operation.

The operating system reads the node’s hardware clock value, Hi t , scales it and adds an offset so as to produce a software clock Ci t = Hi t + that approximately measures real, physical time t for process pi . In other words, when the real time in an absolute frame of reference is t, Ci t is the reading on the software clock. For example,

Ci t could be the 64-bit value of the number of nanoseconds that have elapsed at time t since a convenient reference time. In general, the clock is not completely accurate, so Ci t will differ from t. Nonetheless, if Ci behaves sufficiently well (we shall examine the notion of clock correctness shortly), we can use its value to timestamp any event at pi . Note that successive events will correspond to different timestamps only if the clock resolution – the period between updates of the clock value – is smaller than the time interval between successive events. The rate at which events occur depends on such factors as the length of the processor instruction cycle.

Clock skew and clock drift • Computer clocks, like any others, tend not to be in perfect agreement

Coordinated Universal Time • Computer clocks can be synchronized to external sources of highly accurate time. The most accurate physical clocks use atomic oscillators, whose

drift rate is about one part in 1013. The output of these atomic clocks is used as the standard second has been defined as 9,192,631,770 periods of transition between the two hyperfine levels of the ground state of Caesium-133 (Cs133).

Seconds and years and other time units that we use are rooted in astronomical time. They were originally defined in terms of the rotation of the Earth on its axis and its rotation about the Sun.

However, the period of the Earth’s rotation about its axis is gradually getting longer, primarily because of tidal friction; atmospheric effects and convection currents within the Earth’s core also cause short-term increases and decreases in the period. So astronomical time and atomic time have a tendency to get out of step.

Coordinated Universal Time – abbreviated as UTC (from the French equivalent) – is an international standard for timekeeping. It is based on atomic time, but a so-called ‘leap second’ is inserted – or, more rarely, deleted – occasionally to keep it in step with astronomical time. UTC signals are synchronized and broadcast regularly from landbased

radio stations and satellites covering many parts of the world. For example, in the USA, the radio station WWV broadcasts time signals on several shortwave frequencies.

Satellite sources include the Global Positioning System (GPS).Receivers are available commercially. Compared with ‘perfect’ UTC, the signals received from land-based stations have an accuracy on the order of 0.1–10 milliseconds,

depending on the station used. Signals received from GPS satellites are accurate to about 1 microsecond. Computers with receivers attached can synchronize their clocks with these timing signals.

Synchronizing physical clocks

In order to know at what time of day events occur at the processes in our distributed system – for example, for accountancy purposes – it is necessary to synchronize the processes’ clocks, Ci , with an authoritative, external source of time. This is external synchronization. And if the clocks Ci are synchronized with one another to a known degree of accuracy, then we can measure the interval between two events occurring at different computers by appealing to their local clocks, even though they are not necessarily synchronized to an external source of time. This is internal synchronization.We define these two modes of synchronization more closely as follows, over an interval

of real time I:

External synchronization: For a synchronization bound D 0 , and for a source S of UTC time, S t – Ci t < D, for i = 1 2 N and for all real times t in I. Another way of saying this is that the clocks Ci are accurate to within the bound D.

Internal synchronization: For a synchronization bound D 0 , Ci t – Cj t D for i j = 1

2 N , and for all real times t in I. Another way of saying this is that he clocks Ci agree within the bound D. Clocks that are internally synchronized are not necessarily externally synchronized, since they may drift collectively from an external source of time even though they agree with one another. However, it follows from the definitions that if the system is externally synchronized with a bound D then the same system is internally synchronized with a bound of 2D. Various notions of correctness for clocks have been suggested. It is common to define a hardware clock H to be correct if its drift rate falls within a known bound (a value derived from one supplied by the manufacturer, such as 10–6 seconds/second).

This means that the error in measuring the interval between real times t and t ( t t ) is bounded:

1 – t – t H t – H t 1 + t – t

This condition forbids jumps in the value of hardware clocks (during normal operation). Sometimes we also require our software clocks to obey the condition but a weaker condition of monotonicity may suffice. Monotonicity is the condition that a clock C only ever advances: t t C t C t For example, the UNIX make facility is a tool that is used to compile only those source files that have been modified since they were last compiled. The modification dates of each corresponding pair of source and object files are compared to determine this condition. If a computer whose clock was running fast set its clock back after compiling a source file but before the file was changed, the source file might appear to have been modified prior to the compilation. Erroneously, make will not recompile the source file.

We can achieve monotonicity despite the fact that a clock is found to be running fast. We need only change the rate at which updates are made to the time as given to applications. This can be achieved in software without changing the rate at which the underlying hardware clock ticks – recall that Ci t = Hi t + , where we are free to

choose the values of and . A hybrid correctness condition that is sometimes applied is to require that a clock

obeys the monotonicity condition, and that its drift rate is bounded between synchronization points, but to allow the clock value to jump ahead at synchronization points.

A clock that does not keep to whatever correctness conditions apply is defined to be faulty. A clock’s crash failure is said to occur when the clock stops ticking altogether;

any other clock failure is an arbitrary failure. A historical example of an arbitrary failure is that of a clock with the ‘Y2K bug’, which broke the monotonicity condition by registering the date after 31 December 1999 as 1 January 1900 instead of 2000; another example is a clock whose batteries are very low and whose drift rate suddenly becomes

very large.

Note that clocks do not have to be accurate to be correct, according to the definitions. Since the goal may be internal rather than external synchronization, the criteria for correctness are only concerned with the proper functioning of the clock’s ‘mechanism’, not its absolute setting. We now describe algorithms for external synchronization and for internal

synchronization.

Logical time and logical clocks

From the point of view of any single process, events are ordered uniquely by times shown on the local clock. However, as Lamport [1978] pointed out, since we cannot synchronize clocks perfectly across a distributed system, we cannot in general use physical time to find out the order of any arbitrary pair of events occurring within it. In general, we can use a scheme that is similar to physical causality but that applies in distributed systems to order some of the events that occur at different processes. This ordering is based on two simple and intuitively obvious points: • If two events occurred at the same process pi i = 1 2 N , then they occurred in the order in which pi observes them – this is the order i that we defined above.• Whenever a message is sent between processes, the event of sending the message occurred before the event of receiving the message. Lamport called the partial ordering obtained by generalizing these two relationships the happened-before relation. It is also sometimes known as the relation of causal ordering or potential causal ordering.

We can define the happened-before relation, denoted by , as follows: HB1: If process pi : e i e', then e e .

HB2: For any message m, send(m) receive(m) – where send(m) is the event of sending the message, and receive(m)

is the event of receiving it. HB3: If e, e and e are events such that e e and e e , then e e .

Totally ordered logical clocks • Some pairs of distinct events, generated by different processes, have numerically identical Lamport timestamps. However, we can create a total order on the set of events

that is, one for which all pairs of distinct events are ordered – by taking into account the identifiers of the processes at which events occur. If e is an event occurring at pi with local timestamp Ti , and e is an event occurring at pj with local timestamp Tj , we define the global logical timestamps for these events to be Ti i and Tj j , respectively. And we define Ti i Tj j if and only if either Ti Tj , or Ti = Tj and i j . This ordering has no general physical significance

(because process identiiers are arbitrary), but it is sometimes useful. Lamport used it, for example, to order the entry of processes to a critical section.

Vector clocks • Mattern [1989] and Fidge [1991] developed vector clocks to overcome the shortcoming of Lamport’s clocks: the fact that from L e L e we cannot conclude that e e . . A vector clock for a system of N processes is an array of N

integers. Each process keeps its own vector clock, Vi , which it uses to timestamp local events. Like Lamport timestamps, processes piggyback vector timestamps on the messages they send to one another, and there are simple rules for updating the clocks:

VC1: Initially, Vi j = 0 , for i j = 1 2 N .

VC2: Just before pi timestamps an event, it sets Vi i :=Vi i + 1. VC3: pi includes the value t = Vi in every message it sends.

VC4: When pi receives a timestamp t in a message, it sets Vi j := max Vi j t j , for j = 1 2 N . Taking the componentwise maximum of two vector timestamps in this way is known as a merge operation.For a vector clock Vi , Vi i is the number of events that pi has timestamped, and Vi j j i is the number of events that have occurred at pj that have potentially affected pi . (Process pj may have timestamped more events by this point, but no information has flowed to pi about them in messages as yet.)

Clocks, Events and Process States

o A distributed system consists of a collection P of N processes pi, i = 1,2,… NEach process pi has a state si consisting of its variables (which it transforms as it executes)

o Processes communicate only by messages (via a network)

o Actions of processes: Send, Receive, change own state

o Event: the occurrence of a single action that a process carries out as it executes

o Events at a single process pi, can be placed in a total ordering denoted by the relation →i between the events. i.e.e →i e’ if and only if event e occurs before event e’ at process pi

o A history of process pi: is a series of events ordered by →i

o history(pi) = hi =<ei0, ei1, ei2, …>

Clocks

To timestamp events, use the computer‘s clock • At real time, t, the OS reads the time on the computer‘s hardware clock Hi(t)

§  It calculates the time on its software clock Ci(t)=αHi(t) + β

o   e.g. a 64 bit value giving nanoseconds since some base time

o   Clock resolution: period between updates of the clock value

§  In general, the clock is not completely accurate – but if Ci behaves well enough, it can be used to timestamp events at pi

Skew between computer clocks in a distributed system

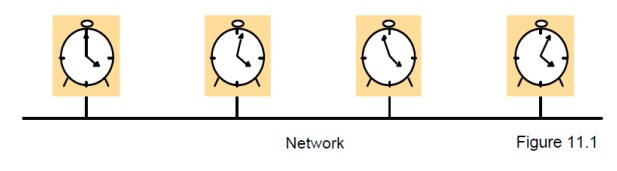
Computer clocks are not generally in perfect agreement

Clock skew: the difference between the times on two clocks (at any instant)

Computer clocks use crystal-based clocks that are subject to physical variations

Clock drift: they count time at different rates and so diverge (frequencies of oscillation differ)

Clock drift rate: the difference per unit of time from some ideal reference clock

Ordinary quartz clocks drift by about 1 sec in 11-12 days. (10-6 secs/sec).

High precision quartz clocks drift rate is about 10-7 or 10-8 secs/sec

Coordinated Universal Time (UTC)

UTC is an international standard for time keeping

It is based on atomic time, but occasionally adjusted to astronomical time

International Atomic Time is based on very accurate physical clocks (drift rate 10-13)

It is broadcast from radio stations on land and satellite (e.g.GPS)

Computers with receivers can synchronize their clocks with these timing signals (by requesting time from GPS/UTC source)

Signals from land-based stations are accurate to about 0.1-10 millisecond

Signals from GPS are accurate to about 1 microsecond