Logical time and logical clocks

Logical time and logical clocks

Instead of synchronizing clocks, event ordering can be used

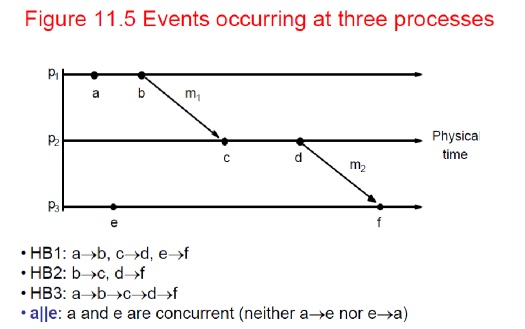
If two events occurred at the same process pi (i = 1, 2, … N) then theyoccurred in the

order observed by pi, that is order →i

when a message, m is sent between two processes, send(m) happened before receive(m)

Lamport[1978] generalized these two relationships into the happened-before relation: e →i e'

HB1: if e →i e' in process pi, then e → e'

HB2: for any message m, send(m) → receive(m)

HB3: if e → e' and e' → e'', then e → e''

Lamport‘s logical clocks

Each process pi has a logical clock Li

a monotonically increasing software counter

not related to a physical clock

Apply Lamport timestamps to events with happened-before relation

LC1: Li is incremented by 1 before each event at process pi

LC2:

when process pi sends message m, it piggybacks t = Li

when pj receives (m,t), it sets Lj := max(Lj, t) and applies LC1 before timestamping the event receive (m)

e →e‘ implies L(e)<L(e‘), but L(e)<L(e') does not imply e→e‘

Totally ordered logical clocks

Some pairs of distinct events, generated by different processes, may have numerically identical Lamport timestamps

Different processes may have same Lamport time

Totally ordered logical clocks

If e is an event occurring at pi with local timestamp Ti, and if e‘ is an event occurring at pj with local timestamp Tj

Define global logical timestamps for the events to be (Ti, i ) and (Tj, j)

Define (Ti, i ) < (Tj, j ) iff

Ti < Tj or

Ti = Tj and i < j

No general physical significance since process identifiers are arbitrary

Vector clocks

Shortcoming of Lamport clocks:

L(e) < L(e') doesn't imply e → e'

Vector clock: an array of N integers for a system of N processes

Each process keeps its own vector clock Vi to timestamp local events

Piggyback vector timestamps on messages

Rules for updating vector clocks:

Vi[i]] is the number of events that pi has timestamped

Viji] ( j≠ i) is the number of events at pj that pi has been affected by VC1: Initially, Vi[ j ] := 0 for pi, j=1.. N (N processes)

VC2: before pi timestamps an event, Vi[ i ] := Vi[ i ]+1 VC3: pi piggybacks t = Vi on every message it sends

VC4: when pi receives a timestamp t, it sets Vi[ j ] := max(Vi[ j ] , t[ j ]) for

j=1..N (merge operation)

Compare vector timestamps

V=V‘ iff V[j] = V‘[j] for j=1..N

V>=V‘ iff V[j] <= V‘[j] for j=1..N

V<V‘ iff V<= V‘ ^ V!=V‘

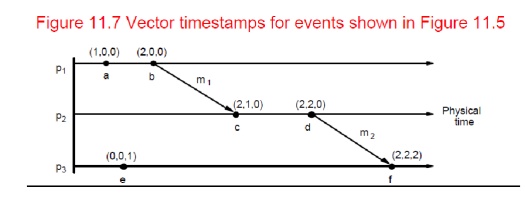
Figure 11.7 shows

a→f since V(a) < V(f)

c || e since neither V(c) <= V(e) nor V(e) <= V(c)