Consensus and related problems

Consensus and related problems

§  Problems of agreement

o   For processes to agree on a value (consensus) after one or more of the processes has proposed what that value should be

o   Covered topics: byzantine generals, interactive consistency, totally ordered multicast

·        The byzantine generals problem: a decision whether multiple armies should attack or retreat, assuming that united action will be more successful than some attacking and some retreating

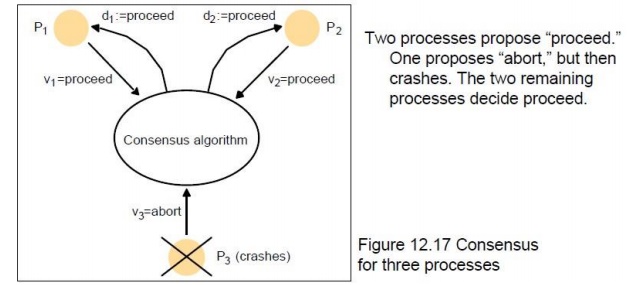
·        Another example might be space ship controllers deciding whether to proceed or abort. Failure handling during consensus is a key concern

§  Assumptions

o   communication (by message passing) is reliable

o   processes may fail

§  Sometimes up to f of the N processes are faulty

·        Consensus Process

·        Each process pi begins in an undecided state and proposes a single value vi, drawn from a set D (i=1…N)

·        Processes communicate with each other, exchanging values

·        Each process then sets the value of a decision variable di and enters the decided state

·        Requirements for Consensus

§  Three requirements of a consensus algorithm

o   Termination: Eventually every correct process sets its decision variable

o   Agreement: The decision value of all correct processes is the same: if pi and pj are correct and have entered the decided state, then di=dj

·        (i,j=1,2, …, N)

o   Integrity: If the correct processes all proposed the same value, then any correct process in the decided state has chosen that value

·        The byzantine generals problem

§  Problem description

o   Three or more generals must agree to attack or to retreat

o   One general, the commander, issues the order

o   Other generals, the lieutenants, must decide to attack or retreat

o   One or more generals may be treacherous

·        A treacherous general tells one general to attack and another to retreat

·        Difference from consensus is that a single process supplies the value to agree on

·        Requirements

o   Termination: eventually each correct process sets its decision variable

o   Agreement: the decision variable of all correct processes is the same

o   Integrity: if the commander is correct, then all correct processes agree on the value that the commander has proposed (but the commander need not be correct)

·        The interactive consistency problem

§  Interactive consistency: all correct processes agree on a vector of values, one for each process. This is called the decision vector

o   Another variant of consensus

§  Requirements

o   Termination: eventually each correct process sets its decision variable

o   Agreement: the decision vector of all correct processes is the same

o   Integrity: if any process is correct, then all correct processes decide the correct value for that process

·        Relating consensus to other problems

§  Consensus (C), Byzantine Generals (BG), and Interactive Consensus (IC) are all problems concerned with making decisions in the context of arbitrary or crash failures

§  We can sometimes generate solutions for one problem in terms of another. For example

o   We can derive IC from BG by running BG N times, once for each process with that process acting as commander

o   We can derive C from IC by running IC to produce a vector of values at each process, then applying a function to the vector‘s values to derive a single value.

o   We can derive BG from C by

§  Commander sends proposed value to itself and each remaining process

§  All processes run C with received values

§  They derive BG from the vector of C values

·        Consensus in a Synchronous System

§  Up to f processes may have crash failures, all failures occurring during f+1 rounds. During each round, each of the correct processes multicasts the values among themselves

·        The algorithm guarantees all surviving correct processes are in a position to agree

·        Note: any process with f failures will require at least f+1 rounds to agree

·        Limits for solutions to Byzantine Generals

§  Some cases of the Byzantine Generals problems have no solutions

o   Lamport et al found that if there are only 3 processes, there is no solution

o   Pease et al found that if the total number of processes is less than three times the number of failures plus one, there is no solution

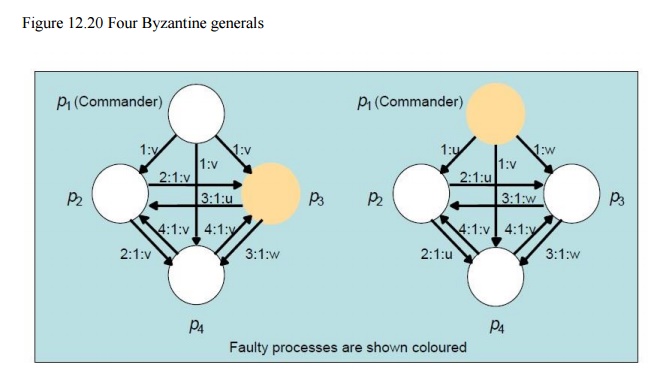
§  Thus there is a solution with 4 processes and 1 failure, if there are two rounds

o   In the first, the commander sends the values

o   while in the second, each lieutenant sends the values it received

·        Asynchronous Systems

·        All solutions to consistency and Byzantine generals problems are limited to synchronous systems

o   Fischer et al found that there are no solutions in an asynchronous system with even one failure

o   This impossibility is circumvented by masking faults or using failure detection

·        There is also a partial solution, assuming an adversary process, based on introducing random values in the process to prevent an effective thwarting strategy. This does not always reach consensus