Stem and Leaf Plot (Stem and Leaf Diagram)

Stem and Leaf Plot (Stem and Leaf Diagram )

The stem and leaf plot is another method of organizing data and is a combination of sorting and graphing. It is an alternative to a tally chart or a grouped frequency distribution. It retains the original data without loss of information. This is also a type of bar chart, in which the numbers themselves would form the bars.

Stem and leaf plot is a type of data representation for numbers, usually like a table with two columns. Generally, stem is the label for left digit (leading digit) and leaf is the label for the right digit (trailing digit) of a number.

For example, the leaf corresponding to the value 63 is 3. The digit to the left of the leaf is called the stem. Here the stem of 63 is 6. Similarly for the number 265, the leaf is 5 and the stem is 26.

The elements of data 252, 255, 260, 262, 276, 276, 276, 283, 289, 298 are expressed in Stem and leaf plot as follows:

From the Stem and Leaf plot, we find easily the smallest number is 252 and the largest number is 298.

Also, in the class 270 – 280 we find 3 items are included and that group has the highest frequency.

The procedure for plotting a Stem and Leaf diagram is illustrated through an example given below:

Example 3.17

Construct a Stem and Leaf plot for the given data.

1.13, 0.72, 0.91, 1.44, 1.03, 0.88, 0.99, 0.73, 0.91, 0.98, 1.21, 0.79, 1.14, 1.19, 1.08, 0.94, 1.06, 1.11, 1.01

Solution:

Step 1: Arrange the data in the ascending order of magnitude:

0.72, 0.73, 0.79, 0.88, 0.91, 0.94, 0.98, 0.99, 1.01,

1.03, 1.06, 1.08, 1.11, 1.13, 1.14, 1.19, 1.21, 1.39, 1.44

Step 2: Separate the data according to the first digit as shown

0.72, 0.73, 0.79

0.88

0.91, 0.91, 0.94, 0.98, 0.99

1.01, 1.03, 1.06, 1.08

1.11, 1.13, 1.14, 1.19

1.21

1.39

1.44

Step 3: Now construct the stem and leaf plot for the above data.

Stem (Leading digits)

Stem (Leading digits)

 0.7

 0.8

 0.9

 1.0

 1.1

 1.2

 1.3

 1.4

Leaves (Trailing digits )

  2 3 9

  8

  1 1 4 8 9

  1 3 6 8

  1 3 4 9

  1

  9

  4

Using a Stem and Leaf plot, finding the Mean, Median, Mode and Range

We know how to create a stem and leaf plot. From this display, let us look at how we can use it to analyze data and draw conclusions. First, let us recall some statistical terms already we used in the earlier classes.

·           The mean is the data value which gives the sum of all the data values, divided by the number of data values.

·           The median is the data value in the middle when the data is ordered from the smallest to the largest.

·           The mode is the data value that occurs most often. On a stem and leaf plot, the mode is the repeated leaf.

·           The range is the difference between the highest and the least data value.

Example 3.18

Determine the mean, median, mode and the range on the stem and leaf plot given below:

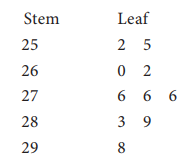
Solution:

From the display, combine the stem with each of its leaves. The values are in the order from the smallest to the largest on the plot. Therefore, keep them in order and list the data values as follows:

252, 255, 260, 262, 276, 276, 276, 283, 289, 298

To determine the mean, add all the data values and then divide the sum by the number of data values.

(252 + 255 + 260 + 262 + 276 + 276 + 276 + 283 + 289 + 298) ÷ 10

=2727 ÷ 10 = 272.7

Mean = 272.7.

The data is already arranged in ascending order. Therefore, identify the number in the middle position of the data. In this case, two data values share the middle position. To find the median, find the mean of these two middle data values.

The two middle numbers are 276 and 27 6.

The median is ( 276 +276 ) ÷ 2 = 276.

The mode is the data value that occurs more frequently. Looking at the stem and leaf plot, we can see the data value 276 appears thrice.

Therefore the mode is 276.

Recall that the range is the difference of the greatest and least values. On the stem and leaf plot, the greatest value is the last value and the smallest value is the first value.

The range is 298 – 252 = 46.