Stefan Boltzmann law and Wien's displacementt law

STEFAN-BOLTZMAN N LAW

Stefan-Boltzmann law, also known as Stefan's law, describes the power radiated from a black body in terms of itste mperature. Specifically, the Stefan-Boltzmann law states that the total energy radiated per unit surface area of a black body across all wavelengths per unit time (also known as the b lack-body radiant exitance or emissive power), J , is directlyproportional to the fou rth power of the black body's thermodynamic temperature T:

WIEN'S DISPLACEMEENT LAW

Wien's displacementt law states that the black body radiation curve for different temperatures peaks at a waveelength inversely proportional to the temper ature. The shift of that peak is a direct consequ ence of the Planck radiation law which des cribes the spectral brightness of black body rad iation as a function of wavelength at any given temperature. However it had been discovered by Wilhelm Wien several years before Max Planck developed that more general equation, and describes the entire shift of the spectrum of black body radiation toward shorter wavelengths as temperature increases.

Formally, Wien's displacement law states that the spectral radiance of black body radiation per unit wavelength, peaks at the wavelength ?_max given by:

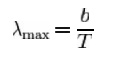
where T is    the    absol ute temperature in    degrees kelvin. b i s    a constant    of  proportionality called Wie n's displacement constant,  equal  to 2.8 977721(26)×10 ^?3 m K.^[1], or more convenien tly to obtain wavelength in microns, b?2900 ?m K. If one is considering the peak of black body emission per unit frequency o r per proportional bandwidth, one must use a different proportionality constant. However the form of the law remains the same: the peak wavelength is inversely proportional to temperature (or the peak frequency is directly proportional to temperature).

Wien's displacement law may be referred to as "Wien's law", a term which is also used for the Wien approximation.