Stack Allocation of Space

Stack Allocation of Space

1 Activation Trees

2 Activation Records

3 Calling Sequences

4 Variable-Length Data on the Stack

5 Exercises for Section 7.2

Almost all compilers for languages that use procedures, functions, or methods as units of user-defined actions manage at least part of their run-time memory as a stack. Each time a procedure¹ is called, space for its local variables is pushed onto a stack, and when the procedure terminates, that space is popped off the stack. As we shall see, this arrangement not only allows space to be shared by procedure calls whose durations do not overlap in time, but it allows us to compile code for a procedure in such a way that the relative addresses of its nonlocal variables are always the same, regardless of the sequence of procedure calls.

1. Activation Trees

Stack allocation would not be feasible if procedure calls, or activations of pro-cedures, did not nest in time. The following example illustrates nesting of procedure calls.

E x a m p l e 7 . 1 : Figure 7.2 contains a sketch of a program that reads nine inte-gers into an array a and sorts them using the recursive quicksort algorithm.

The main function has three tasks. It calls readArray, sets the sentinels, and then calls quicksort on the entire data array. Figure 7.3 suggests a sequence of calls that might result from an execution of the program. In this execution, the call to partition(l,9) returns 4, so a[l] through a[3] hold elements less than its chosen separator value v, while the larger elements are in a [5] through a [9]. •

In this example, as is true in general, procedure activations are nested in time. If an activation of procedure p calls procedure q, then that activation of q must end before the activation of p can end. There are three common cases:

1. The activation of q terminates normally. Then in essentially any language, control resumes just after the point of p at which the call to q was made.

The activation of q, or some procedure q called, either directly or indi-rectly, aborts; i.e., it becomes impossible for execution to continue. In that case, p ends simultaneously with q.

3. The activation of q terminates because of an exception that q cannot han-dle. Procedure p may handle the exception, in which case the activation of q has terminated while the activation of p continues, although not nec-essarily from the point at which the call to q was made. If p cannot handle the exception, then this activation of p terminates at the same time as the activation of q, and presumably the exception will be handled by some other open activation of a procedure.

We therefore can represent the activations of procedures during the running of an entire program by a tree, called an activation tree. Each node corresponds to one activation, and the root is the activation of the "main" procedure that initiates execution of the program. At a node for an activation of procedure p, the children correspond to activations of the procedures called by this activation of p. We show these activations in the order that they are called, from left to right. Notice that one child must finish before the activation to its right can begin.

A Version of Quicksort

The sketch of a quicksort program in Fig. 7.2 uses two auxiliary functions readArray and partition. The function readArray is used only to load the data into the array a. The first and last elements of a are not used for data, but rather for "sentinels" set in the main function. We assume a[0] is set to a value lower than any possible data value, and a[10] is set to a value higher than any data value.

The function partition divides a portion of the array, delimited by the arguments m and n, so the low elements of a[m] through a[n] are at the beginning, and the high elements are at the end, although neither group is necessarily in sorted order. We shall not go into the way partition works, except that it may rely on the existence of the sentinels. One possible algorithm for partition is suggested by the more detailed code in Fig. 9.1.

Recursive procedure  quicksort  first decides  if it  needs  to  sort  more than one element of the array. Note that one element is always "sorted," so quicksort has nothing to do in that case. If there are elements to sort, quicksort first calls partition, which returns an index i to separate the low and high elements. These two groups of elements are then sorted by two recursive calls to quicksort.

E x a m p l e 7 . 2 : One possible activation tree that completes the sequence of calls and returns suggested in Fig. 7.3 is shown in Fig. 7.4. Functions are represented by the first letters of their names. Remember that this tree is only one possibility, since the arguments of subsequent calls, and also the number of calls along any branch is influenced by the values returned by partition. •

The use of a run-time stack is enabled by several useful relationships between the activation tree and the behavior of the program:

            The sequence of procedure calls corresponds to a preorder traversal of the activation tree.

            The sequence of returns corresponds to a postorder traversal of the acti-vation tree.

Suppose that control lies within a particular activation of some procedure, corresponding to a node N of the activation tree. Then the activations that are currently open (live) are those that correspond to node N and its ancestors. The order in which these activations were called is the order in which they appear along the path to N, starting at the root, and they will return in the reverse of that order.

2. Activation Records

Procedure calls and returns are usually managed by a run-time stack called the control stack. Each live activation has an activation record (sometimes called a frame) on the control stack, with the root of the activation tree at the bottom, and the entire sequence of activation records on the stack corresponding to the path in the activation tree to the activation where control currently resides. The latter activation has its record at the top of the stack.

Example 7 . 3 : If control is currently in the activation 0(2,3) of the tree of Fig. 7.4, then the activation record for q(2,3) is at the top of the control stack. Just below is the activation record for 0(1,3), the parent of 0(2,3) in the tree. Below that is the activation record 0(1,9), and at the bottom is the activation record for m, the main function and root of the activation tree.

We shall conventionally draw control stacks with the bottom of the stack higher than the top, so the elements in an activation record that appear lowest on the page are actually closest to the top of the stack.

The contents of activation records vary with the language being imple-mented. Here is a list of the kinds of data that might appear in an activation record (see Fig. 7.5 for a summary and possible order for these elements):

Actual parameters

Returned values

Control link

Access link

Saved machine status

Local data

Temporaries

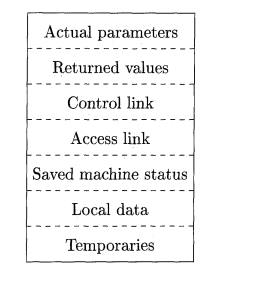
Figure 7.5:  A general activation record

            Temporary values, such as those arising from the evaluation of expres-sions, in cases where those temporaries cannot be held in registers.

            Local data belonging to the procedure whose activation record this is.

            A saved machine status, with information about the state of the machine just before the call to the procedure. This information typically includes the return address (value of the program counter, to which the called procedure must return) and the contents of registers that were used by the calling procedure and that must be restored when the return occurs.

            An "access link" may be needed to locate data needed by the called proce-dure but found elsewhere, e.g., in another activation record. Access links are discussed in Section 7.3.5.

5. A  control link, pointing to the activation record of the caller.

            Space for the return value of the called function, if any. Again, not all called procedures return a value, and if one does, we may prefer to place that value in a register for efficiency.

The actual parameters used by the calling procedure. Commonly, these values are not placed in the activation record but rather in registers, when possible, for greater efficiency. However, we show a space for them to be completely general.

Example 7.4 : Figure 7.6 shows snapshots of the run-time stack as control flows through the activation tree of Fig. 7.4. Dashed lines in the partial trees go to activations that have ended. Since array a is global, space is allocated for it before execution begins with an activation of procedure main, as shown in Fig. 7.6(a).

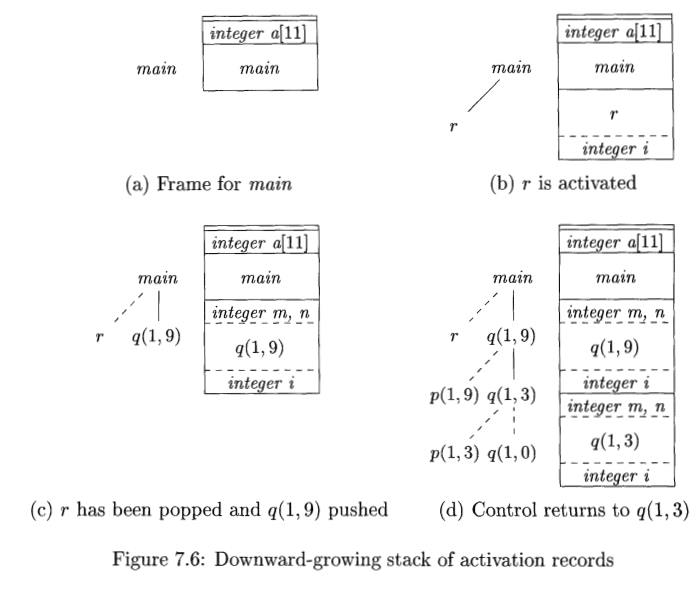
When control reaches the first call in the body of main, procedure r is activated, and its activation record is pushed onto the stack (Fig. 7.6(b)). The activation record for r contains space for local variable i. Recall that the top of stack is at the bottom of diagrams. When control returns from this activation, its record is popped, leaving just the record for main on the stack.

Control then reaches the call to q (quicksort) with actual parameters 1 and 9, and an activation record for this call is placed on the top of the stack, as in Fig. 7.6(c). The activation record for q contains space for the parameters m and n and the local variable i, following the general layout in Fig. 7.5. Notice that space once used by the call of r is reused on the stack. No trace of data local to r will be available to q(l, 9). When q(l, 9) returns, the stack again has only the activation record for main.

Several activations occur between the last two snapshots in Fig. 7.6. A recursive call to g(l,3) was made. Activations p ( l , 3 ) and q(l,0) have begun and ended during the lifetime of q(l, 3), leaving the activation record for q(l, 3) on top (Fig. 7.6(d)). Notice that when a procedure is recursive, it is normal to have several of its activation records on the stack at the same time. •

3. Calling Sequences

Procedure calls are implemented by what are known as calling sequences, which consists of code that allocates an activation record on the stack and enters information into its fields. A return sequence is similar code to restore the state of the machine so the calling procedure can continue its execution after the call.

Calling sequences and the layout of activation records may differ greatly, even among implementations of the same language. The code in a calling se-quence is often divided between the calling procedure (the "caller") and the procedure it calls (the "callee"). There is no exact division of run-time tasks between caller and callee; the source language, the target machine, and the op-erating system impose requirements that may favor one solution over another. In general, if a procedure is called from n different points, then the portion of the calling sequence assigned to the caller is generated n times. However, the portion assigned to the callee is generated only once. Hence, it is desirable to put as much of the calling sequence into the callee as possible — whatever the callee can be relied upon to know. We shall see, however, that the callee cannot know everything.

When designing calling sequences and the layout of activation records, the following principles are helpful:

1.                 Values communicated between caller and callee are generally placed at the beginning of the callee's activation record, so they are as close as possible to the caller's activation record. The motivation is that the caller can compute the values of the actual parameters of the call and place them on top of its own activation record, without having to create the entire activation record of the callee, or even to know the layout of that record.

2.                 Moreover,  it  allows for the  use of procedures that do not  always take the  same  number  or  type  of arguments,  such  as C's p r i n t f  function. The callee knows where to place the return value,  relative to its  own activation record, while however many arguments are present will appear sequentially below that place on the stack.

3.          Fixed-length items are generally placed in the middle. From Fig. 7.5, such items typically include the control link, the access link, and the machine status fields. If exactly the same components of the machine status are saved for each call, then the same code can do the saving and restoring for each. Moreover, if we standardize the machine's status information, then programs such as debuggers will have an easier time deciphering the stack contents if an error occurs.

Items whose size may not be known early enough are placed at the end of the activation record. Most local variables have a fixed length, which can be determined by the compiler by examining the type of the variable. However, some local variables have a size that cannot be determined until the program executes; the most common example is a dynamically sized array, where the value of one of the callee's parameters determines the length of the array. Moreover, the amount of space needed for tempo-raries usually depends on how successful the code-generation phase is in keeping temporaries in registers. Thus, while the space needed for tem-poraries is eventually known to the compiler, it may not be known when the intermediate code is first generated.

4. We must locate the top-of-stack pointer judiciously. A common approach is to have it point to the end of the fixed-length fields in the activation record. Fixed-length data can then be accessed by fixed offsets, known to the intermediate-code generator, relative to the top-of-stack pointer. A consequence of this approach is that variable-length fields in the activation records are actually "above" the top-of-stack. Their offsets need to be calculated at run time, but they too can be accessed from the top-of-stack pointer, by using a positive offset.

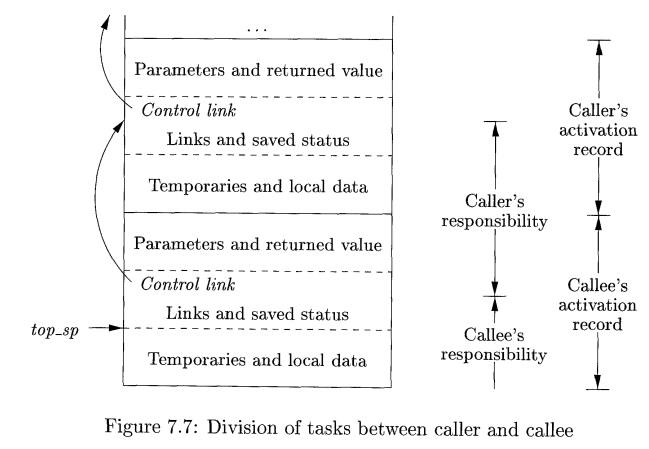
An example of how caller and callee might cooperate in managing the stack is suggested by Fig. 7.7. A register topsp points to the end of the machine-status field in the current top activation record. This position within the callee's activation record is known to the caller, so the caller can be made responsible for setting  topsp before control is passed to the callee.  The calling sequence and its division between caller and callee is as follows:

1.  The caller evaluates the actual parameters.

            The caller stores a return address and the old value of topsp into the callee's activation record. The caller then increments topsp to the po-sition shown in Fig. 7.7. That is, topsp is moved past the caller's local data and temporaries and the callee's parameters and status fields.

            The callee saves the register values and other status information.

            The callee initializes its local data and begins execution.

A suitable, corresponding return sequence is:

1. The callee places the return value next to the parameters, as in Fig. 7.5.

2. Using information in the machine-status field, the callee restores topsp and other registers, and then branches to the return address that the caller placed in the status field.

3.    Although topsp has been decremented, the caller knows where the return value is, relative to the current value of topsp; the caller therefore may use that value.

The above calling and return sequences allow the number of arguments of the called procedure to vary from call to call (e.g., as in C's p r i n t f function). Note that at compile time, the target code of the caller knows the number and types of arguments it is supplying to the callee. Hence the caller knows the size of the parameter area. The target code of the callee, however, must be prepared to handle other calls as well, so it waits until it is called and then examines the parameter field. Using the organization of Fig. 7.7, information describing the parameters must be placed next to the status field, so the callee can find it. For example, in the p r i n t f function of C, the first argument describes the remaining arguments, so once the first argument has been located, the caller can find whatever other arguments there are.

4. Variable-Length Data on the Stack

The run-time memory-management system must deal frequently with the allo-cation of space for objects the sizes of which are not known at compile time, but which are local to a procedure and thus may be allocated on the stack. In modern languages, objects whose size cannot be determined at compile time are allocated space in the heap, the storage structure that we discuss in Section 7.4. However, it is also possible to allocate objects, arrays, or other structures of unknown size on the stack, and we discuss here how to do so. The reason to prefer placing objects on the stack if possible is that we avoid the expense of garbage collecting their space. Note that the stack can be used only for an object if it is local to a procedure and becomes inaccessible when the procedure returns.

A common strategy for allocating variable-length arrays (i.e., arrays whose size depends on the value of one or more parameters of the called procedure) is shown in Fig. 7.8. The same scheme works for objects of any type if they are

local to the procedure called and have a size that depends on the parameters of the call.

In Fig. 7.8, procedure p has three local arrays, whose sizes we suppose cannot be determined at compile time. The storage for these arrays is not part of the activation record for p, although it does appear on the stack. Only a pointer to the beginning of each array appears in the activation record itself. Thus, when p is executing, these pointers are at known offsets from the top-of-stack pointer, so the target code can access array elements through these pointers.

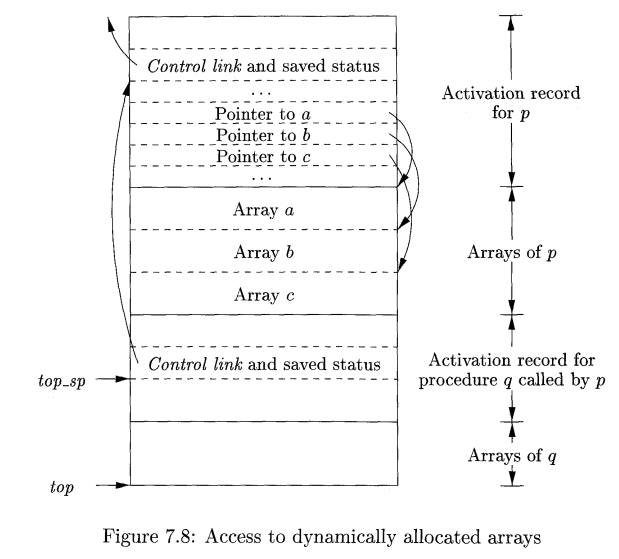
Also shown in Fig. 7.8 is the activation record for a procedure q, called by p. The activation record for q begins after the arrays of p, and any variable-length arrays of q are located beyond that . Access to  the  data on the stack is through two pointers, top  and topsp.

Here,  top marks the actual top  of stack; it points to the position at which the next activation record will begin. The second,  topsp is used to find local, fixed-length fields of the top activation record. For consistency with Fig.  7.7, we shall suppose that  topsp points to the end of the machine-status field.  In Fig.  7.8,  topsp points to the end of this field in the activation record for q. From there, we can find the control-link field for q, which leads us to the place in the activation record for p where topsp pointed when p was on top. The  code to reposition  top  and  topsp  can be generated  at  compile  time,

in terms of sizes that will become known at run time.  When q returns,  topsp can be restored from the saved control link in the activation record for q. The new value of top is (the old unrestored value of) topsp minus the length of the machine-status, control and access link, return-value, and parameter fields (as in Fig. 7.5) in q's activation record. This length is known at compile time to the caller, although it may depend on the caller, if the number of parameters can vary across calls to q.

5. Exercises for Section 7.2

Exercise 7 . 2 . 1 : Suppose that the program of Fig. 7.2 uses a partition function that always picks a[m] as the separator v. Also, when the array a[m],... ,a[n] is reordered, assume that the order is preserved as much as possible. That is, first come all the elements less than v, in their original order, then all elements equal to v, and finally all elements greater than v, in their original order.

            Draw the activation tree when the numbers 9 , 8 , 7 , 6 , 5 , 4 , 3 , 2 , 1 are sorted.

            What is the largest number of activation records that ever appear together on the stack?

Exercise 7 . 2 . 2:  Repeat Exercise 7.2.1 when the initial order of the numbers

is  1,3,5,7,9,2,4,6,8.

Exercise 7 . 2 . 3 : In Fig. 7.9 is C code to compute Fibonacci numbers recur-sively. Suppose that the activation record for / includes the following elements in order: (return value, argument n, local s, local t); there will normally be other elements in the activation record as well. The questions below assume that the initial call is / ( 5 ) .

            Show the complete activation tree.

            What does the stack and its activation records look like the first time / ( l ) is about to return?

c)  What does the stack and its activation records look like the fifth time / ( l ) is about to return?

Exercise 7 . 2 . 4:  Here is a sketch of two C functions / and g:

int f(int x)  { int i; ••• return i+1; ••• }

int g(int y)  { int j; ••• f(j+D ••• 1

That is, function g calls /. Draw the top of the stack, starting with the acti-vation record for g, after g calls /, and / is about to return. You can consider only return values, parameters, control links, and space for local variables; you do not have to consider stored state or temporary or local values not shown in the code sketch. However, you should indicate:

            Which function creates the space on the stack for each element?

            Which function writes the value of each element?

            To which activation record does the element belong?

Exercise 7.2.5 : In a language that passes parameters by reference, there is a that does the function f(x,y) following:

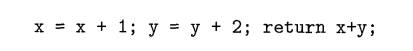
If a is assigned the value 3, and then f ( a , a) is called, what is returned?

Exercise 7 . 2 . 6 :  The C function f is defined by:

Variable a is a pointer to 6; variable 6 is a pointer to c, and c is an integer currently with value 4. If we call f ( c , 6, a), what is returned?