Chapter: Compilers : Principles, Techniques, & Tools : Run-Time Environments
Introduction to Trace-Based Collection
Introduction to Trace-Based Collection
1 A Basic Mark-and-Sweep Collector
2 Basic Abstraction
3 Optimizing Mark-and-Sweep
4 Mark-and-Compact Garbage Collectors
5 Copying collectors
6 Comparing Costs
7 Exercises for Section 7.6
Instead of collecting garbage as it is created, trace-based collectors run periodically to find unreachable objects and reclaim their space. Typically, we run the
trace-based collector whenever the free space is exhausted or its amount drops below some threshold.
We begin this section by introducing the simplest "mark-and-sweep" gar-bage collection algorithm. We then describe the variety of trace-based algo-rithms in terms of four states that chunks of memory can be put in. This section also contains a number of improvements on the basic algorithm, includ-ing those in which object relocation is a part of the garbage-collection function.
1. A Basic Mark-and-Sweep Collector
Mark-and-sweep garbage-collection algorithms are straightforward, stop-the-world algorithms that find all the unreachable objects, and put them on the list of free space. Algorithm 7.12 visits and "marks" all the reachable objects in the first tracing step and then "sweeps" the entire heap to free up unreachable ob-jects. Algorithm 7.14, which we consider after introducing a general framework for trace-based algorithms, is an optimization of Algorithm 7.12. By using an additional list to hold all the allocated objects, it visits the reachable objects only once.
Algorithm 7 . 1 2 : Mark-and-sweep garbage collection.
INPUT : A root set of objects, a heap, and a free list, called Free, with all the unallocated chunks of the heap. As in Section 7.4.4, all chunks of space are marked with boundary tags to indicate their free/used status and size.
OUTPUT : A modified Free list after all the garbage has been removed.
METHOD : The algorithm, shown in Fig. 7.21, uses several simple data struc-tures. List Free holds objects known to be free. A list called Unscanned, holds objects that we have determined are reached, but whose successors we have not yet considered. That is, we have not scanned these objects to see what other

objects can be reached through them. The Unscanned list is empty initially. Additionally, each object includes a bit to indicate whether it has been reached (the reached-bit). Before the algorithm begins, all allocated objects have the reached-bit set to 0.
In line (1) of Fig. 7.21, we initialize the Unscanned list by placing there all the objects referenced by the root set. The reached-bit for these objects is also set to 1. Lines (2) through (7) are a loop, in which we, in turn, examine each object o that is ever placed on the Unscanned list.
The for-loop of lines (4) through (7) implements the scanning of object o. We examine each object d for which we find a reference within o. If d has already been reached (its reached-bit is 1), then there is no need to do anything about d; it either has been scanned previously, or it is on the Unscanned list to be scanned later. However, if d was not reached already, then we need to set its reached-bit to 1 in line (6) and add d to the Unscanned list in line (7). Figure 7.22 illustrates this process. It shows an Unscanned list with four objects. The first object on this list, corresponding to object o in the discussion above, is in the process of being scanned. The dashed lines correspond to the three kinds of objects that might be reached from o:
1. A previously scanned object that need not be scanned again.
2. An object currently on the Unscanned list.
3. An item that is reachable, but was previously thought to be unreached.
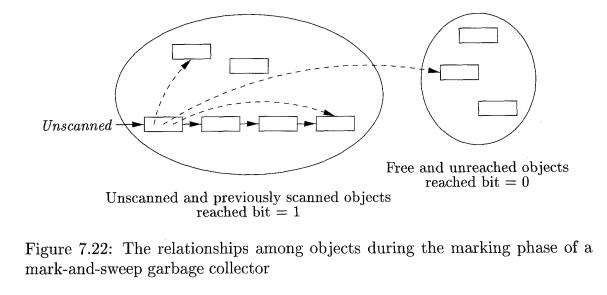
Lines (8) through (11), the sweeping phase, reclaim the space of all the objects that remain unreached at the end of the marking phase. Note that these will include any objects that were on the Free list originally. Because the set of unreached objects cannot be enumerated directly, the algorithm sweeps through the entire heap. Line (10) puts free and unreached objects on the Free list, one at a time. Line (11) handles the reachable objects. We set their reached-bit to 0, in order to maintain the proper preconditions for the next execution of the garbage-collection algorithm. •
2. Basic Abstraction
All trace-based algorithms compute the set of reachable objects and then take the complement of this set. Memory is therefore recycled as follows:
The program or mutator runs and makes allocation requests.
The garbage collector discovers reachability by tracing.
The garbage collector reclaims the storage for unreachable objects.
This cycle is illustrated in Fig. 7.23 in terms of four states for chunks of memory:
Free, Unreached, Unscanned, and Scanned. The state of a chunk might be stored in the chunk itself, or it might be implicit in the data structures used by the garbage-collection algorithm.
While trace-based algorithms may differ in their implementation, they can all be described in terms of the following states:
Free. A chunk is in the Free state if it is ready to be allocated. Thus, a Free chunk must not hold a reachable object.
Unreached. Chunks are presumed unreachable, unless proven reachable by tracing. A chunk is in the Unreached state at any point during garbage
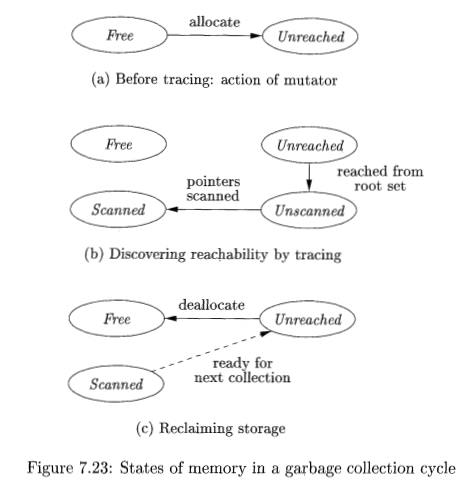
collection if its reachability has not yet been established. Whenever a chunk is allocated by the memory manager, its state is set to Unreached as illustrated in Fig. 7.23(a). Also, after a round of garbage collection, the state of a reachable object is reset to Unreached to get ready for the next round; see the transition from Scanned to Unreached, which is shown dashed to emphasize that it prepares for the next round.
Unscanned. Chunks that are known to be reachable are either in state Unscanned or state Scanned. A chunk is in the Unscanned state if it is
known to be reachable, but its pointers have not yet been scanned. The transition to Unscanned from Unreached occurs when we discover that a chunk is reachable; see Fig. 7.23(b).
Scanned. Every Unscanned object will eventually be scanned and tran-sition to the Scanned state. To scan an object, we examine each of the pointers within it and follow those pointers to the objects to which they refer. If a reference is to an Unreached object, then that object is put in the Unscanned state. When the scan of an object is completed, that object is placed in the Scanned state; see the lower transition in Fig. 7.23(b). A Scanned object can only contain references to other Scanned or Unscanned objects, and never to Unreached objects.
When no objects are left in the Unscanned state, the computation of reach-ability is complete. Objects left in the Unreached state at the end are truly unreachable. The garbage collector reclaims the space they occupy and places the chunks in the Free state, as illustrated by the solid transition in Fig. 7.23(c). To get ready for the next cycle of garbage collection, objects in the Scanned state are returned to the Unreached state; see the dashed transition in Fig. 7.23(c). Again, remember that these objects really are reachable right now. The Un-reachable state is appropriate because we shall want to start all objects out in this state when garbage collection next begins, by which time any of the currently reachable objects may indeed have been rendered unreachable.
Example 7.13: Let us see how the data structures of Algorithm 7.12 relate to the four states introduced above. Using the reached-bit and membership on lists Free and Unscanned, we can distinguish among all four states. The table of Fig. 7.24 summarizes the characterization of the four states in terms of the data structure for Algorithm 7.12.

3. Optimizing Mark-and-Sweep
The final step in the basic mark-and-sweep algorithm is expensive because there is no easy way to find only the unreachable objects without examining the entire heap. An improved algorithm, due to Baker, keeps a list of all allocated objects. To find the set of unreachable objects, which we must return to free space, we take the set difference of the allocated objects and the reached objects.
Algorithm 7 . 14: Baker's mark-and-sweep collector.
INPUT: A root set of objects, a heap, a free list Free, and a list of allocated objects, which we refer to as Unreached.
OUTPUT: Modified lists Free and Unreached, which holds allocated objects.
METHOD: In this algorithm, shown in Fig. 7.25, the data structure for garbage collection is four lists named Free, Unreached, Unscanned, and Scanned, each of which holds all the objects in the state of the same name. These lists may be implemented by embedded, doubly linked lists, as was discussed in Section 7.4.4. A reached-bit in objects is not used, but we assume that each object contains bits telling which of the four states it is in. Initially, Free is the free list maintained by the memory manager, and all allocated objects are on the Unreached list (also maintained by the memory manager as it allocates chunks to objects).

Lines (1) and (2) initialize Scanned to be the empty list, and Unscanned to have only the objects reached from the root set. Note that these objects were presumably on the list Unreached and must be removed from there. Lines (3) through (7) are a straightforward implementation of the basic marking algo-rithm, using these lists. That is, the for-loop of lines (5) through (7) examines the references in one unscanned object o, and if any of those references o' have not yet been reached, line (7) changes o' to the Unscanned state.
At the end, line (8) takes those objects that are still on the Unreached list and deallocates their chunks, by moving them to the Free list. Then, line (9) takes all the objects in state Scanned, which are the reachable objects, and reinitializes the Unreached list to be exactly those objects. Presumably, as the memory manager creates new objects, those too will be added to the Unreached list and removed from the Free list. •
In both algorithms of this section, we have assumed that chunks returned to the free list remain as they were before deallocation. However, as discussed in Section 7.4.4, it is often advantageous to combine adjacent free chunks into larger chunks. If we wish to do so, then every time we return a chunk to the free list, either at line (10) of Fig. 7.21 or line (8) of Fig. 7.25, we examine the chunks to its left and right, and merge if one is free.
4. Mark-and-Compact Garbage Collectors
Relocating collectors move reachable objects around in the heap to eliminate memory fragmentation. It is common that the space occupied by reachable ob-jects is much smaller than the freed space. Thus, after identifying all the holes, instead of freeing them individually, one attractive alternative is to relocate all the reachable objects into one end of the heap, leaving the entire rest of the heap as one free chunk. After all, the garbage collector has already analyzed every reference within the reachable objects, so updating them to point to the new locations does not require much more work. These, plus the references in the root set, are all the references we need to change.
Having all the reachable objects in contiguous locations reduces fragmen-tation of the memory space, making it easier to house large objects. Also, by making the data occupy fewer cache lines and pages, relocation improves a pro-gram's temporal and spatial locality, since new objects created at about the same time are allocated nearby chunks. Objects in nearby chunks can bene-fit from prefetching if they are used together. Further, the data structure for maintaining free space is simplified; instead of a free list, all we need is a pointer free to the beginning of the one free block.
Relocating collectors vary in whether they relocate in place or reserve space
ahead of time for the relocation:
• A mark-and-compact collector, described in this section, compacts objects in place. Relocating in place reduces memory usage.
The more efficient and popular copying collector in Section 7.6.5 moves objects from one region of memory to another. Reserving extra space for relocation allows reachable objects to be moved as they are discovered.
The mark-and-compact collector in Algorithm 7.15 has three phases:
First is a marking phase, similar to that of the mark-and-sweep algorithms described previously.
Second, the algorithm scans the allocated section of the heap and com- putes a new address for each of the reachable objects. New addresses are assigned from the low end of the heap, so there are no holes between reach-able objects. The new address for each object is recorded in a structure called NewLocation.
Finally, the algorithm copies objects to their new locations, updating all references in the objects to point to the corresponding new locations. The
needed addresses are found in NewLocation.
A l g o r i t h m 7 . 1 5 : A mark-and-compact garbage collector.
INPUT: A root set of objects, a heap, and free, a pointer marking the start of free space.
OUTPUT: The new value of pointer free.
METHOD: The algorithm is in Fig. 7.26; it uses the following data structures: 1. An Unscanned list, as in Algorithm 7.12.
Reached bits in all objects, also as in Algorithm 7.12. To keep our de-scription simple, we refer to objects as "reached" or "unreached," when we mean that their reached-bit is 1 or 0, respectively. Initially, all objects are unreached.
The pointer free, which marks the beginning of unallocated space in the heap.
The table NewLocation. This structure could be a hash table, search tree, or another structure that implements the two operations:
(a) Set NewLocation{o) to a new address for object o.
(b) Given object o, get the value of NewLocation(o).
We shall not concern ourselves with the exact structure used, although you may assume that NewLocation is a hash table, and therefore, the "set" and "get" operations are each performed in average constant time, independent of how many objects are in the heap.
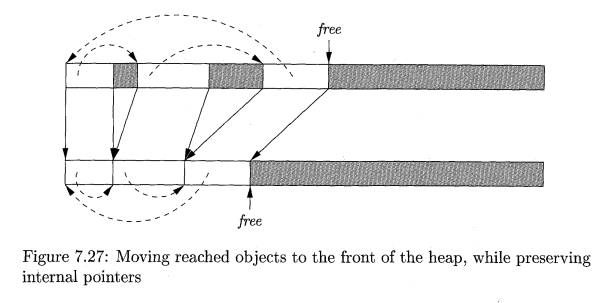
The first, or marking, phase of lines (1) through (7) is essentially the same as the first phase of Algorithm 7.12. The second phase, lines (8) through (12), visits each chunk in the allocated part of the heap, from the left, or low end. As a result, chunks are assigned new addresses that increase in the same order as their old addresses. This ordering is important, since when we relocate objects, we can do so in a way that assures we only move objects left, into space that was formerly occupied by objects we have moved already.
Line (8) starts the free pointer at the low end of the heap. In this phase, we use free to indicate the first available new address. We create a new address only for those objects o that are marked as reached. Object o is given the next available address at line (10), and at line (11) we increment free by the amount of storage that object o requires, so free again points to the beginning of free space.
In the final phase, lines (13) through (17), we again visit the reached objects, in the same from-the-left order as in the second phase. Lines (15) and (16) replace all internal pointers of a reached object o by their proper new values, using the NewLocation table to determine the replacement. Then, line (17) moves the object o, with the revised internal references, to its new location. Finally, lines (18) and (19) retarget pointers in the elements of the root set that are not themselves heap objects, e.g., statically allocated or stack-allocated objects. Figure 7.27 suggests how the reachable objects (those that are not shaded) are moved down the heap, while the internal pointers are changed to point to the new locations of the reached objects.
5. Copying collectors
A copying collector reserves, ahead of time, space to which the objects can move, thus breaking the dependency between tracing and finding free space.

The memory space is partitioned into two semispaces, A and B. The mutator allocates memory in one semispace, say A, until it fills up, at which point the mutator is stopped and the garbage collector copies the reachable objects to the other space, say B. When garbage collection completes, the roles of the semispaces are reversed. The mutator is allowed to resume and allocate objects in space B, and the next round of garbage collection moves reachable objects to space A. The following algorithm is due to C. J. Cheney.
Algorithm 7 . 16: Cheney's copying collector.
INPUT: A root set of objects, and a heap consisting of the From semispace, containing allocated objects, and the To semispace, all of which is free.
OUTPUT: At the end, the To semispace holds the allocated objects. A free pointer indicates the start of free space remaining in the To semispace. The From semispace is completely free.
METHOD: The algorithm is shown in Fig. 7.28. Cheney's algorithm finds reachable objects in the From semispace and copies them, as soon as they are reached, to the To semispace. This placement groups related objects together and may improve spatial locality.
Before examining the algorithm itself, which is the function CopyingCollector m. Fig. 7.28, consider the auxiliary function LookupNewLocation in lines (11) through (16). This function takes an object o and finds a new location for it in the To space if o has no location there yet. All new locations are recorded in a structure NewLocation, and a value of N U L L indicates o has no assigned location.5 As in Algorithm 7.15, the exact form of structure NewLocation may vary, but it is fine to assume that it is a hash table.
If we find at line (12) that o has no location, then it is assigned the beginning of the free space within the To semispace, at line (13). Line (14) increments the free pointer by the amount of space taken by o, and at line (15) we copy o from the From space to the To space. Thus, the movement of objects from one semispace to the other occurs as a side effect, the first time we look up the new location for the object. Regardless of whether the location of o was or was not previously established, line (16) returns the location of o in the To space.
Now, we can consider the algorithm itself. Line (2) establishes that none of the objects in the From space have new addresses yet. At line (3), we initialize two pointers, unscanned and free, to the beginning of the To semispace. Pointer free will always indicate the beginning of free space within the To space. As we add objects to the To space, those with addresses below unscanned will be in the Scanned state, while those between unscanned and free are in the Unscanned

state. Thus, free always leads unscanned, and when the latter catches up to the former, there are no more Unscanned objects, and we are done with the garbage collection. Notice that we do our work within the To space, although all references within objects examined at line (8) lead us back to the From space.
Lines (4) and (5) handle the objects reachable from the root set. Note that as a side effect, some of the calls to LookupNewLocation at line (5) will increase free, as chunks for these objects are allocated within To. Thus, the loop of lines (6) through (10) will be entered the first time it is reached, unless there are no objects referenced by the root set (in which case the entire heap is garbage). This loop then scans each of the objects that has been added to To and is in the Unscanned state. Line (7) takes the next unscanned object, o. Then, at lines (8) and (9), each reference within o is translated from its value in the From semispace to its value in the To semispace. Notice that, as a side effect, if a reference within o is to an object we have not reached previously, then the call to LookupNewLocation at line (9) creates space for that object in the To space and moves the object there. Finally, line (10) increments unscanned to point to the next object, just beyond o in the To space.
6. Comparing Costs
Cheney's algorithm has the advantage that it does not touch any of the un-reachable objects. On the other hand, a copying garbage collector must move the contents of all the reachable objects. This process is especially expensive for large objects and for long-lived objects that survive multiple rounds of garbage collection. We can summarize the running time of each of the four algorithms described in this section, as follows. Each estimate ignores the cost of processing the root set.
• Basic Mark-and-Sweep (Algorithm 7.12): Proportional to the number of chunks in the heap.
• Baker's Mark-and-Sweep (Algorithm 7.14): Proportional to the number of reached objects.
» Basic Mark-and-Compact (Algorithm 7.15): Proportional to the number of chunks in the heap plus the total size of the reached objects.
• Cheney's Copying Collector (Algorithm 7.16): Proportional to the total size of the reached objects.
7. Exercises for Section 7.6
Exercise 7 . 6 . 1 : Show the steps of a mark-and-sweep garbage collector on
Fig. 7.19 with the pointer A ->• B deleted.
Fig. 7.19 with the pointer A -> C deleted.
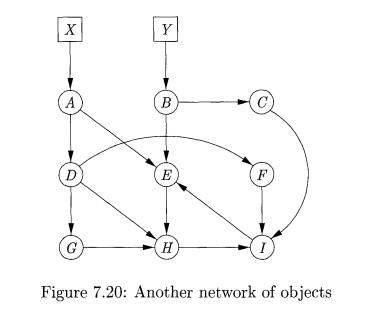
c) Fig. 7.20 with the pointer A-t D deleted.
d) Fig. 7.20 with the object B deleted.
Exercise 7 . 6 . 2: The Baker mark-and-sweep algorithm moves objects among four lists: Free, Unreached, Unscanned, and Scanned. For each of the object networks of Exercise 7.6.1, indicate for each object the sequence of lists on which it finds itself from just before garbage collection begins until just after it finishes.
Exercise 7 . 6 . 3 : Suppose we perform a mark-and-compact garbage collection on each of the networks of Exercise 7.6.1. Also, suppose that
Each object has size 100 bytes, and
Initially, the nine objects in the heap are arranged in alphabetical order, starting at byte 0 of the heap.
What is the address of each object after garbage collection?
E x e r c i s e 7.6.4: Suppose we execute Cheney's copying garbage collection al-gorithm on each of the networks of Exercise 7.6.1. Also, suppose that
Each object has size 100 bytes,
The unscanned list is managed as a queue, and when an object has more than one pointer, the reached objects are added to the queue in alpha-betical order, and
Hi. The From semispace starts at location 0, and the To semispace starts at location 10,000.
What is the value of NewLocation(o) for each object o that remains after garbage collection?
Related Topics