Access to Nonlocal Data on the Stack

Access to Nonlocal Data on the Stack

1 Data Access Without Nested Procedures

2 Issues With Nested Procedures

3 A Language With Nested Procedure Declarations

4 Nesting Depth

5 Access Links

6 Manipulating Access Links

7 Access Links for Procedure Parameters

8 Displays

9 Exercises for Section 7.3

In this section, we consider how procedures access their data. Especially im-portant is the mechanism for finding data used within a procedure p but that does not belong to p. Access becomes more complicated in languages where procedures can be declared inside other procedures. We therefore begin with the simple case of C functions, and then introduce a language, ML, that permits both nested function declarations and functions as "first-class objects;" that is, functions can take functions as arguments and return functions as values. This capability can be supported by modifying the implementation of the run-time stack, and we shall consider several options for modifying the stack frames of Section 7.2.

1. Data Access Without Nested Procedures

In the C family of languages, all variables are defined either within a single function or outside any function ("globally"). Most importantly, it is impossible to declare one procedure whose scope is entirely within another procedure. Rather, a global variable v has a scope consisting of all the functions that follow the declaration of v, except where there is a local definition of the identifier v. Variables declared within a function have a scope consisting of that function only, or part of it, if the function has nested blocks, as discussed in Section 1.6.3.

For languages that do not allow nested procedure declarations, allocation of storage for variables and access to those variables is simple:

            Global variables are allocated static storage. The locations of these vari-ables remain fixed and are known at compile time. So to access any variable that is not local to the currently executing procedure, we simply use the statically determined address.

2. Any other name must be local to the activation at the top of the stack.

We may access these variables through the  topsp pointer of the stack.

An important benefit of static allocation for globals is that declared proce-dures may be passed as parameters or returned as results (in C, a pointer to the function is passed), with no substantial change in the data-access strategy. With the C static-scoping rule, and without nested procedures, any name non-local to one procedure is nonlocal to all procedures, regardless of how they are activated. Similarly, if a procedure is returned as a result, then any nonlocal name refers to the storage statically allocated for it.

2. Issues With Nested Procedures

Access becomes far more complicated when a language allows procedure dec-larations to be nested and also uses the normal static scoping rule; that is, a procedure can access variables of the procedures whose declarations surround its own declaration, following the nested scoping rule described for blocks in Section 1.6.3. The reason is that knowing at compile time that the declaration of p is immediately nested within q does not tell us the relative positions of their activation records at run time. In fact, since either p or q or both may be recursive, there may be several activation records of p and/or q on the stack.

Finding the declaration that applies to a nonlocal name x in a nested pro-cedure p is a static decision; it can be done by an extension of the static-scope rule for blocks. Suppose x is declared in the enclosing procedure q. Finding the relevant activation of q from an activation of p is a dynamic decision; it re-quires additional run-time information about activations. One possible solution to this problem is to use "access links," which we introduce in Section 7.3.5.

3. A Language With Nested Procedure Declarations

The C family of languages, and many other familiar languages do not support nested procedures, so we introduce one that does. The history of nested pro-cedures in languages is long. Algol 60, an ancestor of C, had this capability, as did its descendant Pascal, a once-popular teaching language. Of the later languages with nested procedures, one of the most influential is ML, and it is this language whose syntax and semantics we shall borrow (see the box on "More about ML" for some of the interesting features of ML):

            ML is a functional language, meaning that variables, once declared and initialized, are not changed. There are only a few exceptions, such as the

array, whose elements can be changed by special function calls.

• Variables are defined, and have their unchangeable values initialized, by a statement of the form:

v a l (name) = (expression)

•  Functions are defined using the syntax:

fun (name)  ( (arguments) )                   = (body)

•  For function bodies we shall use let-statements of the form:

let (list of definitions) in (statements) end  The definitions are normally v a l or fun statements. The scope of each such definition consists of all following definitions, up to the in, and all the statements up to the end. Most importantly, function definitions can be nested. For example, the body of a function p can contain a let-statement that includes the definition of another (nested) function q. Similarly, q can have function definitions within its own body, leading to arbitrarily deep nesting of function

4. Nesting Depth

Let us give nesting depth 1 to procedures that are not nested within any other procedure. For example, all C functions are at nesting depth 1. However, if a procedure p is defined immediately within a procedure at nesting depth i, then give p the nesting depth i +

E x a m p l e 7 . 5: Figure 7.10 contains a sketch in ML of our running quicksort example. The only function at nesting depth 1 is the outermost function, sort, which reads an array a of 9 integers and sorts them using the quicksort algo-rithm. Defined within sort, at line (2), is the array a itself. Notice the form of the ML declaration. The first argument of a r r a y says we want the array to have 11 elements; all ML arrays are indexed by integers starting with 0, so this array is quite similar to the C array a from Fig. 7.2. The second argument of a r r a y says that initially, all elements of the array a hold the value 0. This choice of initial value lets the ML compiler deduce that a is an integer array, since 0 is an integer, so we never have to declare a type for a.

More About ML

In addition to being almost purely functional, ML presents a number of other surprises to the programmer who is used to C and its family.

            ML supports higher-order functions. That is, a function can take functions as arguments, and can construct and return other func-tions. Those functions, in turn, can take functions as arguments, to any level.

ML has essentially no iteration, as in C's for- and while-statements, for instance. Rather, the effect of iteration is achieved by recur sion. This approach is essential in a functional language, since we cannot change the value of an iteration variable like i in " f o r ( i = 0 ; i<10; i++)" of C. Instead, ML would make i a function argument, and the function would call itself with progressively higher values of i until the limit was reached.

• ML supports lists and labeled tree structures as primitive data types.

 ML does not require declaration of variable types. Rather, it deduces types at compile time, and treats it as an error if it cannot. For example, v a l x = 1 evidently makes x have integer type, and if we also see v a l y = 2*x, then we know y is also an integer.

Also declared within sort are several functions: readArray, exchange, and quicksort. On lines (4) and (6) we suggest that readArray and exchange each access the array a. Note that in ML, array accesses can violate the functional nature of the language, and both these functions actually change values of a's elements, as in the C version of quicksort. Since each of these three functions is defined immediately within a function at nesting depth 1, their nesting depths are all 2.

Lines (7) through (11) show some of the detail of quicksort. Local value v, the pivot for the partition, is declared at line (8). Function partition is defined at line (9). In line (10) we suggest that partition accesses both the array a and the pivot value v, and also calls the function exchange. Since partition is  defined immediately within a function at nesting depth 2, it is at depth 3. Line

(11) suggests that quicksort accesses variables a and v, the function partition, and itself recursively. 

Line (12) suggests that the outer function sort accesses a and calls the two procedures readArray and quicksort. •

5. Access Links

A direct implementation of the normal static scope rule for nested functions is obtained by adding a pointer called the access link to each activation record. If procedure p is nested immediately within procedure q in the source code, then the access link in any activation of p points to the most recent activation of q. Note that the nesting depth of q must be exactly one less than the nesting depth of p. Access links form a chain from the activation record at the top of the stack to a sequence of activations at progressively lower nesting depths. Along this chain are all the activations whose data and procedures are accessible to the currently executing procedure.

Suppose that the procedure p at the top of the stack is at nesting depth n_p, and p needs to access x, which is an element defined within some procedure q that surrounds p and has nesting depth nq. Note that nq =< np, with equality only if p and q are the same procedure. To find x, we start at the activation record for p at the top of the stack and follow the access link np — nq times, from activation record to activation record. Finally, we wind up at an activation record for q, and it will always be the most recent (highest) activation record for q that currently appears on the stack. This activation record contains the element x that we want. Since the compiler knows the layout of activation records, x will be found at some fixed offset from the position in g's activation record that we can reach by following the last access link.

E x a m p l e 7 . 6 : Figure 7.11 shows a sequence of stacks that might result from execution of the function sort of Fig. 7.10. As before, we represent function names by their first letters, and we show some of the data that might appear in the various activation records, as well as the access link for each activation. In Fig. 7.11(a), we see the situation after sort has called readArray to load input into the array a and then called quicksort(l, 9) to sort the array. The access link from quicksort(l, 9) points to the activation record for sort, not because sort called quicksort but because sort is the most closely nested function surrounding quicksort in the program of Fig. 7.10.

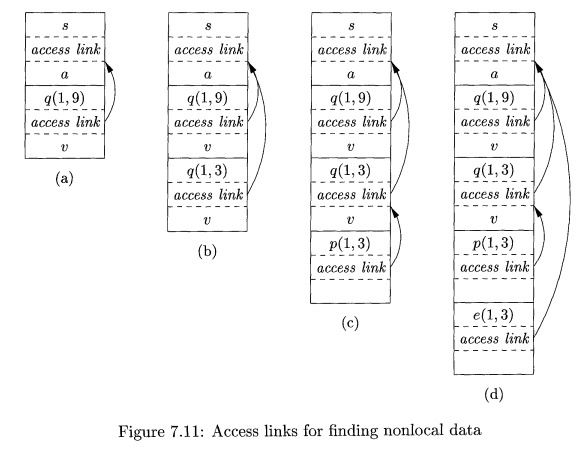
In successive steps of Fig. 7.11 we see a recursive call to quicksort(l, 3), followed by a call to partition, which calls exchange. Notice that quicksort(l, 3)'s access link points to sort, for the same reason that quicksort(l, 9)'s does.

In Fig. 7.11(d), the access link for exchange bypasses the activation records for quicksort and partition, since exchange is nested immediately within sort. That arrangement is fine, since exchange needs to access only the array a, and the two elements it must swap are indicated by its own parameters i and j.

6. Manipulating Access Links

How are access links determined? The simple case occurs when a procedure call is to a particular procedure whose name is given explicitly in the procedure call. The harder case is when the call is to a procedure-parameter; in that case, the particular procedure being called is not known until run time, and the nesting depth of the called procedure may differ in different executions of the call. Thus, let us first consider what should happen when a procedure q calls procedure p, explicitly. There are three cases:

1. Procedure p is at a higher nesting depth than q. Then p must be defined immediately within q, or the call by q would not be at a position that is within the scope of the procedure name p. Thus, the nesting depth of p is exactly one greater than that of q, and the access link from p must lead to q. It is a simple matter for the calling sequence to include a step that places in the access link for p a pointer to the activation record of q. Examples include the call of quicksort by sort to set up Fig. 7.11(a), and the call of partition by quicksort to create Fig. 7.11(c).

            The call is recursive, that is, p = q2 Then the access link for the new acti-vation record is the same as that of the activation record below it. An ex-

ample is the call of quicksort(l, 3) by quicksort(l, 9) to set up Fig. 7.11(b).

3. The nesting depth np of p is less than the nesting depth nq of q. In order for the call within q to be in the scope of name p, procedure q must be nested within some procedure r, while p is a procedure defined immediately within r. The top activation record for r can therefore be found by following the chain of access links, starting in the activation record for q, for nq — np + 1 hops. Then, the access link for p must go to this activation of r.

Example 7 . 7: For an example of case (3), notice how we-go from Fig. 7.11(c) to Fig. 7.11(d). The nesting depth 2 of the called function exchange is one less than the depth 3 of the calling function partition. Thus, we start at the activation record for partition and follow 3 - 2 + 1 = 2 access links, which takes us from partition's activation record to that of quicksort(l,S) to that of sort.

The access link for exchange therefore goes to the activation record for sort, as we see in Fig. 7.11(d).

An equivalent way to discover this access link is simply to follow access links for n _q - n _p hops, and copy the access link found in that record. In our example, we would go one hop to the activation record for quicksort(l, 3) and copy its access link to sort. Notice that this access link is correct for exchange, even though exchange is not in the scope of quicksort, these being sibling functions nested within sort.

7. Access Links for Procedure Parameters

When a procedure p is passed to another procedure q as a parameter, and q then calls its parameter (and therefore calls p in this activation of q), it is possible that q does not know the context in which p appears in the program. If so, it is impossible for q to know how to set the access link for p. The solution to this problem is as follows: when procedures are used as parameters, the caller needs to pass, along with the name of the procedure-parameter, the proper access link for that parameter.

The caller always knows the link, since if p is passed by procedure r as an actual parameter, then p must be a name accessible to r, and therefore, r can determine the access link for p exactly as if p were being called by r directly. That is, we use the rules for constructing access links given in Section 7.3.6.

E x a m p l e 7 . 8: In Fig. 7.12 we see a sketch of an ML function a that has functions b and c nested within it. Function b has a function-valued parameter f, which it calls. Function c defines within it a function d, and c then calls b with actual parameter d.

Let us trace what happens when a is executed. First, a calls c, so we place an activation record for c above that for a on the stack. The access link for c points to the record for a, since c is defined immediately within a. Then c calls b(d). The calling sequence sets up an activation record for b, as shown in Fig. 7.13(a).

Within this activation record is the actual parameter d and its access link, which together form the value of formal parameter f in the activation record for b. Notice that c knows about d, since d is defined within c, and therefore c passes a pointer to its own activation record as the access link. No matter where d was defined, if c is in the scope of that definition, then one of the three rules of Section 7.3.6 must apply, and c can provide the link.

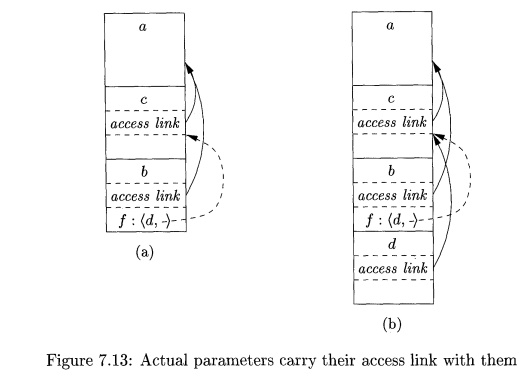
Now, let us look at what b does. We know that at some point, it uses its parameter f, which has the effect of calling d. An activation record for d appears on the stack, as shown in Fig. 7.13(b). The proper access link to place in this activation record is found in the value for parameter /; the link is to the activation record for c, since c immediately surrounds the definition of d. Notice that b is capable of setting up the proper link, even though b is not in the scope of c's definition. •

8. Displays

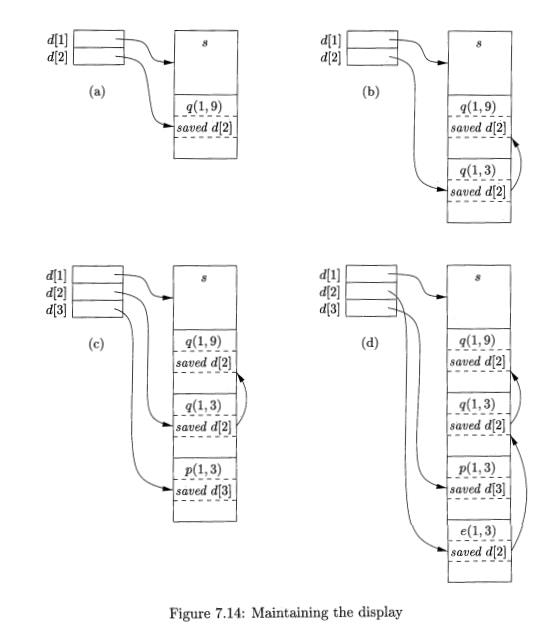
One problem with the access-link approach to nonlocal data is that if the nesting depth gets large, we may have to follow long chains of links to reach the data we need. A more efficient implementation uses an auxiliary array d, called the display, which consists of one pointer for each nesting depth. We arrange that, at all times, d[i] is a pointer to the highest activation record on the stack for any procedure at nesting depth i. Examples of a display are shown in Fig. 7.14.

For instance, in Fig. 7.14(d), we see the display d, with d[l] holding a pointer to the activation record for sort , the highest (and only) activation record for a function at nesting depth 1. Also, d[2] holds a pointer to the activation record for exchange, the highest record at depth 2, and d[3] points to partition, the highest record at depth 3.

The advantage of using a display is that if procedure p is executing, and it needs to access element x belonging to some procedure q, we need to look only in d[i], where i is the nesting depth of q; we follow the pointer d[i] to the activation record for q, wherein x is found at a known offset. The compiler knows what i is, so it can generate code to access x using d[i] and the offset of

x from the top of the activation record for q. Thus, the code never needs to follow a long chain of access links.

In order to maintain the display correctly, we need to save previous values of display entries in new activation records. If procedure p at depth n_p is called, and its activation record is not the first on the stack for a procedure at depth n_p, then the activation record for p needs to hold the previous value of d[n_p], while d[n_p] itself is set to point to this activation of p. When p returns, and its activation record is removed from the stack, we restore d[n_p] to have its value prior to the call of p.

Example 7.9 : Several steps of manipulating the display  are illustrated in Fig. 7.14. In Fig. 7.14(a), sort at depth 1 has called quicksort(l, 9) at depth 2.

The activation record for quicksort has a place to store the old value of d[2], indicated as saved d[2], although in this case since there was no prior activation record at depth 2, this pointer is null.

In Fig. 7.14(b), quicksort(l, 9) calls quicksort(l, 3). Since the activation records for both calls are at depth 2, we must store the pointer to quicksort(l, 9), which was in d[2], in the record for quicksort(l, 3). Then, d[2] is made to point to      quicksort(l,  3).

Next, partition is called. This function is at depth 3, so we use the slot d[3] in the display for the first time, and make it point to the activation record for partition. The record for partition has a slot for a former value of d[3], but in this case there is none, so the pointer remains null. The display and stack at this time are shown in Fig. 7.14(c).

Then, partition calls  exchange.  That function is at depth 2,  so its activation record stores the old pointer d[2], which goes to the activation record for quicksort(l, 3).  Notice that  the display pointers "cross"; that  is, d[3] points further down the stack than d[2] does. However, that is a proper situation; exchange can only access its own data and that of sort, via d[l].

9. Exercises for Section 7.3

Exercise 7.3.1 : In Fig. 7.15 is a ML function main that computes Fibonacci numbers in a nonstandard way. Function f ibO will compute the nth Fibonacci number for any n > 0. Nested within in is f i b l , which computes the nth Fibonacci number on the assumption n > 2, and nested within f i b l is f ib2, which assumes n > 4. Note that neither f i b l nor f ib2 need to check for the basis cases. Show the stack of activation records that result from a call to main, up until the time that the first call (to f i b O ( l ) ) is about to return. Show the access link in each of the activation records on the stack.

Exercise 7.3.2 : Suppose that we implement the functions of Fig. 7.15 using a display. Show the display at the moment the first call to f i b O ( l ) is about to return. Also, indicate the saved display entry in each of the activation records on the stack at that time.