Chapter: Compilers : Principles, Techniques, & Tools : Run-Time Environments
Heap Management
Heap Management
1 The Memory Manager
2 The Memory Hierarchy of a
Computer
3 Locality in Programs
4 Reducing Fragmentation
5 Manual Deallocation Requests
6 Exercises for Section 7.4
The heap is the portion of the store that is used for data that lives
indefinitely, or until the program explicitly deletes it. While local variables
typically become inaccessible when their procedures end, many languages enable
us to create objects or other data whose existence is not tied to the procedure
activation that creates them. For example, both C + + and Java give the
programmer new to create objects that may be passed — or pointers to them may
be passed — from procedure to procedure, so they continue to exist long after
the procedure that created them is gone. Such objects are stored on a heap.
In this section, we discuss the memory
manager, the subsystem that allo-cates and deallocates space within the
heap; it serves as an interface between application programs and the operating
system. For languages like C or C + + that deallocate chunks of storage manually (i.e., by explicit statements
of the program, such as f r e e or delete ) , the memory manager is also
responsible for implementing deallocation.
In Section 7.5, we discuss garbage
collection, which is the process of finding spaces within the heap that are
no longer used by the program and can therefore be reallocated to house other
data items. For languages like Java, it is the garbage collector that
deallocates memory. When it is required, the garbage collector is an important
subsystem of the memory manager.
1. The Memory Manager
The memory manager keeps track of all the free space in heap storage at
all times. It performs two basic functions:
• Allocation. When a program requests memory for a variable or object,3 the memory manager produces a
chunk of contiguous heap memory of the requested size. If possible, it
satisfies an allocation request using free space in the heap; if no chunk of
the needed size is available, it seeks to increase the heap storage space by
getting consecutive bytes of virtual memory from the operating system. If space
is exhausted, the memory manager passes that information back to the
application program.
• Deallocation. The memory manager returns deallocated space to the pool of free space, so it can reuse the
space to satisfy other allocation requests. Memory managers typically do not
return memory to the operating sys-tem, even if the program's heap usage drops.
Memory management would be simpler if (a) all allocation requests were for chunks of the
same size, and (b)
storage were released predictably, say, first-allocated first-deallocated.
There are some languages, such as
Lisp, for which condition
(a) holds; pure Lisp
uses only one data element — a two- pointer cell — from which all
data structures are built. Condition (b) also holds in some situations,
the most common being data that can be allocated on the run-time stack. However, in most languages, neither (a) nor
(b) holds in general. Rather, data elements of different sizes are allocated,
and there is no good way to predict the lifetimes of all allocated objects.
Thus, the memory manager must be prepared to service, in any order,
allo-cation and deallocation requests of any size, ranging from one byte to as
large as the program's entire address space.
Here are the properties we desire of memory managers:
• Space Efficiency. A
memory manager should
minimize the total
heap space needed by a program. Doing so allows larger programs to run
in a fixed virtual address space. Space efficiency is achieved by minimizing
"fragmentation," discussed in Section 7.4.4.
• Program Efficiency. A memory manager should make good use of the memory subsystem to allow programs to run faster. As we shall see
in Section 7.4.2, the time taken to execute an instruction can vary widely
depending on where objects are placed in memory. Fortunately, programs tend to
exhibit "locality," a phenomenon discussed in Section 7.4.3, which
refers to the nonrandom clustered way in which typical programs access memory.
By attention to the placement of objects in memory, the memory manager can make
better use of space and, hopefully, make the program run faster.
• Low Overhead. Because memory allocations and deallocations are fre-quent operations in
many programs, it is important that these operations be as efficient as
possible. That is, we wish to minimize the overhead
— the fraction of execution time spent performing allocation and
dealloca-tion. Notice that the cost of allocations is dominated by small
requests; the overhead of managing large objects is less important, because it
usu-ally can be amortized over a larger amount of computation.
2. The
Memory Hierarchy of a Computer
Memory management and compiler optimization must be done with an
aware-ness of how memory behaves. Modern machines are designed so that
program-mers can write correct programs without concerning themselves with the
details of the memory subsystem. However, the efficiency of a program is
determined not just by the number of instructions executed, but also by how
long it takes to execute each of these instructions. The time taken to execute
an instruction can vary significantly, since the time taken to access different
parts of memory can vary from nanoseconds to milliseconds. Data-intensive
programs can there-fore benefit significantly from optimizations that make good
use of the memory subsystem. As we shall see in Section 7.4.3, they can take
advantage of the phenomenon of "locality" — the nonrandom behavior of
typical programs.
The large variance in memory access times is due to the fundamental
limitation in hardware technology; we can build small and fast storage, or
large and slow storage, but not storage that is both large and fast. It is simply impossible today to build
gigabytes of storage with nanosecond access times, which is how fast
high-performance processors run. Therefore, practically all modern computers
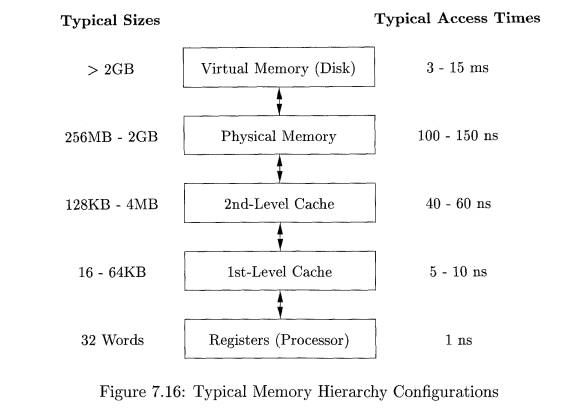
arrange their storage as a memory hierarchy. A memory hierarchy, as shown in
Fig. 7.16, consists of a series of storage elements, with the smaller faster
ones "closer" to the processor, and the larger slower ones further
away.
Typically, a processor has a small number of registers, whose contents
are under software control. Next, it has one or more levels of cache, usually
made out of static RAM, that are kilobytes to several megabytes in size. The
next level of the hierarchy is the physical (main) memory, made out of hundreds
of megabytes or gigabytes of dynamic RAM. The physical memory is then backed up
by virtual memory, which is implemented by gigabytes of disks. Upon a memory
access, the machine first looks for the data in the closest (lowest-level)
storage and, if the data is not there, looks in the next higher level, and so
on.
Registers are scarce, so register usage is tailored for the specific
applications and managed by the code that a compiler generates. All the other
levels of the hierarchy are managed automatically; in this way, not only is the
programming task simplified, but the same program can work effectively across
machines with different memory configurations. With each memory access, the
machine searches each level of the memory in succession, starting with the
lowest level, until it locates the data. Caches are managed exclusively in
hardware, in order to keep up with the relatively fast RAM access times.
Because disks are rela
tively slow, the virtual memory is managed by the operating system, with
the assistance of a hardware structure known as the "translation lookaside
buffer."
Data is transferred as blocks of contiguous storage. To amortize the
cost of access, larger blocks are used with the slower levels of the hierarchy.
Be-tween main memory and cache, data is transferred in blocks known as cache lines, which are typically from 32 to 256 bytes long. Between
virtual memory (disk) and main
memory, data is transferred in blocks known as pages, typically between 4K and 64K bytes in size.
3. Locality in Programs
Most programs exhibit a high degree of locality; that is, they spend most of their time
executing a relatively small fraction of the code and touching only a small
fraction of the data. We say that a
program has temporal locality if the
memory locations it accesses are likely to be accessed again within a short
period of time. We say that a program has spatial
locality if memory locations close to the location accessed are likely also
to be accessed within a short period of time.
The conventional wisdom is that programs spend 90% of their time
executing 10% of the code. Here is why:
Programs often contain many instructions that are never executed. Pro-grams
built with components and libraries use only a small fraction of the provided
functionality. Also as requirements change and programs evolve, legacy systems
often contain many instructions that are no longer used.
Static and Dynamic RAM
Most random-access memory is dynamic,
which means that it is built of very simple electronic circuits that lose their
charge (and thus "forget" the bit
they were storing) in a
short time. These circuits need to
be refreshed — that is, their
bits read and rewritten — periodically. On the other
hand, static RAM is designed with a more
complex circuit for each bit, and consequently the bit stored can stay
indefinitely, until it is changed. Evidently, a chip can store more bits if it
uses dynamic-RAM circuits than if it uses static-RAM circuits, so we tend to
see large main memories of the dynamic variety, while smaller memories, like
caches, are made from static circuits.
• Only a small fraction of the code that could be invoked is actually
executed in a typical run of the program. For example, instructions to handle
illegal inputs and exceptional cases, though critical to the correctness of the
program, are seldom invoked on any particular run.
The typical program spends most
of its time executing innermost loops and tight recursive cycles in a program.
Locality allows us to take advantage of the memory hierarchy of a modern
computer, as shown in Fig. 7.16. By placing the most common instructions and
data in the fast-but-small storage, while leaving the rest in the
slow-but-large storage, we can lower the average memory-access time of a
program significantly.
It has been found that many programs exhibit both temporal and spatial
locality in how they access both instructions and data. Data-access patterns,
however, generally show a greater variance than instruction-access patterns.
Policies such as keeping the most recently used data in the fastest hierarchy
work well for common programs but may not work well for some data-intensive
programs — ones that cycle through very large arrays, for example.
We often cannot tell, just from looking at the code, which sections of
the code will be heavily used, especially for a particular input. Even if we
know which instructions are executed heavily, the fastest cache often is not
large enough to hold all of them at the same time. We must therefore adjust the
contents of the fastest storage dynamically and use it to hold instructions
that are likely to be used heavily in the near future.
Optimization Using the Memory Hierarchy
The policy of keeping the most recently used instructions in the cache
tends to work well; in other words, the past is generally a good predictor of
future memory usage. When a new
instruction is executed, there is a high probability that the next instruction
also will be executed. This phenomenon
is an example of spatial locality. One effective technique to improve the
spatial lo-cality of instructions is to have the compiler place basic blocks
(sequences of instructions that are always executed sequentially) that are
likely to follow each other contiguously — on the same page, or even the same
cache line, if possi-ble. Instructions belonging to the same loop or same
function also have a high probability of being executed together.4
We can also improve the temporal and spatial locality of data accesses
in a program by changing the data layout or the order of the computation. For
example, programs that visit large amounts of data repeatedly, each time
per-forming a small amount of computation, do not perform well. It is better if
we can bring some data from a slow level of the memory hierarchy to a faster
level (e.g., disk to main memory) once, and perform all the necessary
computations on this data while it resides at the faster level. This concept
can be applied recursively to reuse data in physical memory, in the caches and
in the registers.
4. Reducing Fragmentation
At the beginning of program execution, the heap is one contiguous unit
of free space. As the program allocates and deallocates memory, this space is
broken up into free and used chunks of memory, and the free chunks need not
reside in a contiguous area of the heap. We refer to the free chunks of memory
as holes. With each allocation
request, the memory manager must place
the requested chunk of memory into a large-enough hole. Unless a hole of
exactly the right size is found, we need to split
some hole, creating a yet smaller hole.
With each deallocation request, the freed chunks of memory are added
back to the pool of free space. We
coalesce contiguous holes into larger holes, as the holes can only get smaller
otherwise. If we are not careful, the
memory may end up getting fragmented, consisting of large numbers of small,
noncontiguous holes. It is then possible that no hole is large enough to
satisfy a future request, even though there may be sufficient aggregate free
space.
Best - Fit and Next - Fit Object Placement
We reduce fragmentation by controlling how the memory manager places new
objects in the heap. It has been found empirically that a good strategy for
mini-mizing fragmentation for real-life programs is to allocate the requested
memory in the smallest available hole that is large enough. This best-fit algorithm tends to spare the
large holes to satisfy subsequent, larger requests. An alternative, called first-fit, where an object is placed in
the first (lowest-address) hole in which it fits, takes less time to place
objects, but has been found inferior to best-fit in overall performance.
To implement best-fit placement more efficiently, we can separate free
space into bins, according to their
sizes. One practical idea is to have many more bins for the smaller sizes,
because there are usually many more small objects. For example, the Lea memory
manager, used in the GNU C compiler gcc, aligns all chunks to 8-byte
boundaries. There is a bin for every multiple of 8-byte chunks from 16 bytes to
512 bytes. Larger-sized bins are logarithmically spaced (i.e., the minimum size
for each bin is twice that of the previous bin), and within each of these bins
the chunks are ordered by their size. There is always a chunk of free space
that can be extended by requesting more pages from the operating system. Called
the wilderness chunk, this chunk is
treated by Lea as the largest-sized bin because of its extensibility.
Binning makes it easy to find the best-fit chunk.
If, as for small sizes requested
from the Lea memory manager, there is a bin for chunks of that size only, we
may take any chunk from that bin.
For sizes that do not have a
private bin, we find the one bin that is allowed to include chunks of the
desired size. Within that bin, we can use
either a first-fit or a best-fit strategy; i.e., we either look for and
select the first chunk that is sufficiently large or, we spend more time and
find the smallest chunk that is sufficiently large. Note that when the fit is
not exact, the remainder of the chunk will generally need to be placed in a bin
with smaller sizes.
• However, it may be that the
target bin is empty, or all chunks in that bin are too small to satisfy the
request for space. In that case, we
simply repeat the search, using the bin for the next larger size(s). Eventually, we either find a chunk we can
use, or we reach the "wilderness"
chunk, from which we can surely obtain the needed space, possibly by
going to the operating system and getting additional pages for the heap.
While best-fit placement tends to improve space utilization, it may not
be the best in terms of spatial locality. Chunks allocated at about the same
time by a program tend to have similar reference patterns and to have similar
lifetimes. Placing them close together thus improves the program's spatial
locality. One useful adaptation of the best-fit algorithm is to modify the
placement in the case when a chunk of the exact requested size cannot be found.
In this case, we use a next-fit
strategy, trying to allocate the object in the chunk that has last been split,
whenever enough space for the new object remains in that chunk. Next-fit also
tends to improve the speed of the allocation operation.
M a n a g i n g and Coalescing Free Space
When an object is deallocated manually, the memory manager must make its
chunk free, so it can be allocated again. In some circumstances, it may also be
possible to combine (coalesce) that
chunk with adjacent chunks of the heap, to form a larger chunk. There is an
advantage to doing so, since we can always use a large chunk to do the work of
small chunks of equal total size, but many small chunks cannot hold one large
object, as the combined chunk could.
If we keep a bin for chunks of one fixed size, as Lea does for small
sizes, then we may prefer not to coalesce adjacent blocks of that size into a
chunk of double the size. It is simpler to keep all the chunks of one size in
as many pages as we need, and never coalesce them. Then, a simple
allocation/deallocation scheme is to keep a bitmap, with one bit for each chunk
in the bin. A 1 indicates the chunk is occupied; 0 indicates it is free. When a
chunk is deallocated, we change its 1 to a 0. When we need to allocate a chunk,
we find any chunk with a 0 bit, change that bit to a 1, and use the
corresponding chunk. If there are no free chunks, we get a new page, divide it
into chunks of the appropriate size, and extend the bit vector.
Matters are more complex when the heap is managed as a whole, without
binning, or if we are willing to coalesce adjacent chunks and move the
resulting chunk to a different bin if necessary. There are two data structures
that are useful to support coalescing of adjacent free blocks:
• Boundary Tags. At both the low and high ends of each chunk,
whether free or allocated, we keep vital
information. At both ends, we keep a free/used bit that tells whether or not
the block is currently allocated (used) or available (free). Adjacent to each
free/used bit is a count of the total number of bytes in the chunk.
• A Doubly Linked, Embedded Free List. The free chunks (but not the
allocated chunks) are also linked in a doubly linked list. The pointers for
this list are within the blocks themselves, say adjacent to the boundary tags
at either end. Thus, no additional space is needed for the free list, although
its existence does place a lower bound on how small chunks can get; they must
accommodate two boundary tags and two pointers, even if the object is a single
byte. The order of chunks on the free list is left unspecified. For example,
the list could be sorted by size, thus facilitating best-fit placement.
Example 7 . 1 0 : Figure 7.17
shows part of a heap with three adjacent chunks, A, B, and C. Chunk B: of size
100, has just been deallocated and returned to the free list. Since we know the
beginning (left end) of 5, we also know
the end of the chunk that happens to be immediately to B's left, namely A in
this example. The free/used bit at the right end of A is currently 0, so A
too is free. We may therefore coalesce A
and B into one chunk of 300 bytes.
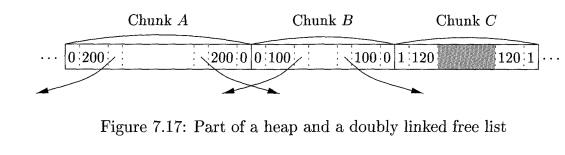
It might be the case that chunk C, the chunk immediately to B's right, is also free, in which case we can
combine all of A, B, and C. Note that if
we always coalesce chunks when we can, then there can never be two adjacent
free chunks, so we never have to look further than the two chunks adjacent to
the one being deallocated. In the current case, we find the beginning of C by starting at the left end of B, which we know, and finding the total
number of bytes in B, which is found
in the left boundary tag of B and is
100 bytes. With this information, we find the right end of B and the beginning of the chunk to its right. At that point, we
examine the free/used bit of C and
find that it is 1 for used; hence, C
is not available for coalescing.
Since we must coalesce A and B, we need to remove one of them from
the free list. The doubly linked free-list structure lets us find the chunks
before and after each of A and B. Notice that it should not be assumed
that physical neighbors A and B are also adjacent on the free list.
Knowing the chunks preceding and following
A and B on the free list, it is straightforward to manipulate pointers on
the list to replace A and B by one coalesced chunk. •
Automatic garbage collection can eliminate fragmentation altogether if
it moves all the allocated objects to contiguous storage. The interaction
between garbage collection and memory management is discussed in more detail in
Sec-tion 7.6.4.
5. Manual Deallocation Requests
We close this section with manual memory management, where the
programmer must explicitly arrange for the deallocation of data, as in C and C
+ + . Ideally, any storage that will no longer be accessed should be deleted.
Conversely, any storage that may be referenced must not be deleted.
Unfortunately, it is hard to enforce either of these properties. In addition to
considering the difficulties with manual deallocation, we shall describe some
of the techniques programmers use to help with the difficulties.
Problems with Manual Deallocation
Manual memory management is error-prone. The common mistakes take two
forms: failing ever to delete data that cannot be referenced is called a memory-leak error, and referencing
deleted data is a
dangling-pointer-dereference error.
It is hard for programmers to tell if a program will never refer to some stor-age in the future, so the first
common mistake is not deleting storage that will never be referenced. Note that
although memory leaks may slow down the exe-cution of a program due to
increased memory usage, they do not affect program correctness, as long as the
machine does not run out of memory. Many pro-grams can tolerate memory leaks,
especially if the leakage is slow. However, for long-running programs, and
especially nonstop programs like operating systems or server code, it is
critical that they not have leaks.
Automatic garbage collection gets rid of memory leaks by deallocating
all the garbage. Even with automatic garbage collection, a program may still
use more memory than necessary. A programmer may know that an object will never
be referenced, even though references to that object exist somewhere. In that
case, the programmer must deliberately remove references to objects that will
never be referenced, so the objects can be deallocated automatically.
Being overly zealous about deleting objects can lead to even worse
problems than memory leaks. The second common mistake is to delete some storage
and then try to refer to the data in the deallocated storage. Pointers to
storage that has been deallocated are known as
dangling pointers. Once the freed
storage has been reallocated to a new
variable, any read, write,
or deallocation via the dangling pointer can produce seemingly random
effects. We refer to any operation, such as read, write, or deallocate, that
follows a pointer and tries to use the object it points to, as dereferencing the pointer.
Notice that reading through a dangling pointer may return an arbitrary
value. Writing through a dangling pointer arbitrarily changes the value of the
new variable. Deallocating a dangling pointer's storage means that the storage
of the new variable may be allocated to yet another variable, and actions on
the old and new variables may conflict with each other.
Unlike memory leaks, dereferencing a dangling pointer after the freed
storage is reallocated almost always creates a program error that is hard to
debug. As a result, programmers are more inclined not to deallocate a variable
if they are not certain it is unreferencable.
A related form of programming error is to access an illegal address.
Common examples of such errors include dereferencing null pointers and
accessing an out-of-bounds array element. It is better for such errors to be
detected than to have the program silently corrupt the results. In fact, many
security violations exploit programming errors of this type, where certain
program inputs allow unintended access to data, leading to a "hacker"
taking control of the program and machine. One antidote is to have the compiler
insert checks with every access, to make sure it is within bounds. The
compiler's optimizer can discover and remove those checks that are not really
necessary because the optimizer can deduce that the access must be within
bounds.
An Example: Purify
Rational's Purify is one of the most popular commercial tools that helps
programmers find memory access errors and memory leaks in programs. Purify
instruments binary code by adding additional instructions to check for errors
as the program executes. It keeps a map of memory to indicate where all the
freed and used spaces are. Each allocated object is bracketed with extra space;
accesses to unallocated locations or to spaces between objects are flagged as
errors. This approach finds some dangling pointer references, but not when the
memory has been reallocated and a valid object is sitting in its place. This
approach also finds some out-of-bound array accesses, if they happen to land in
the space inserted at the end of the objects.
Purify also finds memory leaks at the end of a program execution. It
searches the contents of all the allocated objects for possible pointer values.
Any object without a pointer to it is a leaked chunk of memory. Purify reports
the amount of memory leaked and the locations of the leaked objects. We may
compare Purify to a "conservative garbage collector," which will be
discussed in Section 7.8.3. and machine. One antidote is to have the compiler
insert checks with every access, to make sure it is within bounds. The
compiler's optimizer can discover and remove those checks that are not really
necessary because the optimizer can deduce that the access must be within
bounds.
Programming Conventions and
Tools
We now present a few of the most popular conventions and tools that have
been developed to help programmers cope with the complexity in managing memory:
• Object ownership is useful when an object's lifetime can be statically rea-soned about.
The idea is to associate an owner
with each object at all times. The owner is a pointer to that object,
presumably belonging to some function invocation. The owner (i.e., its
function) is responsible for either deleting the object or for passing the
object to another owner. It is possible to have other, nonowning pointers to
the same object; these pointers can be overwritten any time, and no deletes
should ever be ap-plied through them. This convention eliminates memory leaks,
as well as attempts to delete the same object twice. However, it does not help
solve the dangling-pointer-reference problem, because it is possible to follow
a nonowning pointer to an object that has been deleted.
Reference counting is useful when an object's lifetime needs to be deter-mined dynamically.
The idea is to associate a count with each dynamically allocated object.
Whenever a reference to the object is created, we incre-ment the reference
count; whenever a reference is removed, we decrement the reference count. When
the count goes to zero, the object can no longer be referenced and can
therefore be deleted. This technique, however, does not catch useless, circular
data structures, where a collection of objects cannot be accessed, but their
reference counts are not zero, since they refer to each other. For an
illustration of this problem, see Example 7.11. Reference counting does
eradicate all dangling-pointer references, since there are no outstanding references
to any deleted objects. Reference counting is expensive because it imposes an
overhead on every operation that stores a pointer.
• Region-based allocation is useful for collections of objects whose lifetimes are tied to specific phases in a computation.When objects are
created to be used only within some step of a computation, we can allocate all
such objects in the same region. We then delete the entire region once that
computation step completes. This region-based
allocation technique has limited applicability. However, it is very
efficient whenever it can be used; instead of deallocating objects one at a
time, it deletes all objects in the region in a wholesale fashion.
6. Exercises for Section 7.4
Exercise 7 . 4 . 1 : Suppose
the heap consists of seven chunks, starting at address 0. The sizes of the
chunks, in order, are 80, 30, 60, 50, 70, 20, 40 bytes. When we place an object
in a chunk, we put it at the high end if there is enough space remaining to
form a smaller chunk (so that the smaller chunk can easily remain on the linked
list of free space). However, we cannot tolerate chunks of fewer that 8 bytes,
so if an object is almost as large as the selected chunk, we give it the entire
chunk and place the object at the low end of the chunk.
If we request space for objects of the following sizes: 32, 64, 48, 16,
in that order, what does the free space list look like after satisfying the
requests, if the method of selecting chunks is
First fit.
Best fit.
Related Topics