Specification of Tokens

SPECIFICATION OF TOKENS

There are 3 specifications of tokens:

1)Strings

2) Language

3)Regular expression

Strings and Languages

v                 An alphabet or character class is a finite set of symbols.

v                 A string over an alphabet is a finite sequence of symbols drawn from that alphabet.

v                 A language is any countable set of strings over some fixed alphabet.

In language theory, the terms "sentence" and "word" are often used as synonyms for

"string." The length of a string s, usually written |s|, is the number of occurrences of symbols in s. For example, banana is a string of length six. The empty string, denoted ε, is the string of length zero.

Operations on strings

The following string-related terms are commonly used:

1.                 A prefix of string s is any string obtained by removing zero or more symbols from the end of string s. For example, ban is a prefix of banana.

2.                 A suffix of string s is any string obtained by removing zero or more symbols from the beginning of s. For example, nana is a suffix of banana.

3.                 A substring of s is obtained by deleting any prefix and any suffix from s. For example, nan is a substring of banana.

4.  The proper prefixes, suffixes, and substrings of a string s are those prefixes, suffixes, and substrings, respectively of s that are not ε or not equal to s itself.

5.  A subsequence of s is any string formed by deleting zero or more not necessarily consecutive positions of s

6.  For example, baan is a subsequence of banana.

Operations on languages:

The following are the operations that can be applied to languages:

1. Union

2. Concatenation

3. Kleene closure

4. Positive closure

The following example shows the operations on strings: Let L={0,1} and S={a,b,c}

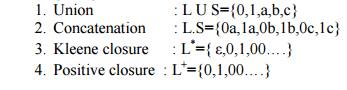
Regular Expressions

·                 Each regular expression r denotes a language L(r).

·                 Here are the rules that define the regular expressions over some alphabet Σ and the languages that those expressions denote:

1.ε is a regular expression, and L(ε) is { ε }, that is, the language whose sole member is the empty string.

2. If ‘a’ is a symbol in Σ, then ‘a’ is a regular expression, and L(a) = {a}, that is, the language with one string, of length one, with ‘a’ in its one position.

3.Suppose r and s are regular expressions denoting the languages L(r) and L(s). Then, a) (r)|(s) is a regular expression denoting the language L(r) U L(s).

b) (r)(s) is a regular expression denoting the language L(r)L(s). c) (r)* is a regular expression denoting (L(r))*.

d) (r) is a regular expression denoting L(r).

4.The unary operator * has highest precedence and is left associative.

5.Concatenation has second highest precedence and is left associative.

6. | has lowest precedence and is left associative.

Regular set

A language that can be defined by a regular expression is called a regular set. If two regular expressions r and s denote the same regular set, we say they are equivalent and write r = s.

There are a number of algebraic laws for regular expressions that can be used to manipulate into equivalent forms.

For instance, r|s = s|r is commutative; r|(s|t)=(r|s)|t is associative.

Regular Definitions

Giving names to regular expressions is referred to as a Regular definition. If Σ is an alphabet of basic symbols, then a regular definition is a sequence of definitions of the form

d_l → r ₁

d₂ → r₂

………

d_n → r_n

1.Each d_i is a distinct name.

2.Each r_i is a regular expression over the alphabet Σ U {d_l, d₂,. . . , d_i-l}.

Example: Identifiers is the set of strings of letters and digits beginning with a letter. Regular

definition for this set:

letter → A | B | …. | Z | a | b | …. | z | digit → 0 | 1 | …. | 9

id → letter ( letter | digit ) *

Shorthands

Certain constructs occur so frequently in regular expressions that it is convenient to introduce notational short hands for them.

1. One or more instances (+):

- The unary postfix operator + means “ one or more instances of” .

-  If r is a regular expression that denotes the language L(r), then ( r )⁺ is a regular expression that denotes the language (L (r ))⁺

- Thus the regular expression a⁺ denotes the set of all strings of one or more a’s.

- The operator ⁺ has the same precedence and associativity as the operator ^*.

2. Zero or one instance ( ?):

- The unary postfix operator ? means “zero or one instance of”.

- The notation r? is a shorthand for r | ε.

-  If ‘r’ is a regular expression, then ( r )? is a regular expression that denotes the language

3. Character Classes:

- The notation [abc] where a, b and c are alphabet symbols denotes the regular expression a | b | c.

- Character class such as [a – z] denotes the regular expression a | b | c | d | ….|z.

- We can describe identifiers as being strings generated by the regular expression, [A–Za–z][A– Za–z0–9]*

Non-regular Set

A language which cannot be described by any regular expression is a non-regular set. Example: The set of all strings of balanced parentheses and repeating strings cannot be described by a regular expression. This set can be specified by a context-free grammar.