A Language For Specifying Lexical Analyzer

A LANGUAGE FOR SPECIFYING LEXICAL ANALYZER

There is a wide range of tools for constructing lexical analyzers.

Lex

YACC

Lex is a computer program that generates lexical analyzers. Lex is commonly used with the yacc parser generator.

Creating a lexical analyzer

•                          First, a specification of a lexical analyzer is prepared by creating a program lex.l in the Lex language. Then, lex.l is run through the Lex compiler to produce a C program lex.yy.c.

•                          Finally, lex.yy.c is run through the C compiler to produce an object progra m a.out, which is the lexical analyzer that transforms an input stream into a sequence of tokens.

Fig1.11 Creating a lexical analyzer with lex

Lex Specification

A Lex program consists of three parts:

{ definitions }

%%

{ rules }

%%

{ user subroutines }

Definitions include declarations of variables, constants, and regular definitions

Ø    Rules are statements of the form

p₁ {action₁}

p₂ {action₂}

…

p_n {action_n}

where p_i is regular expression and action_i describes what action the lexical analyzer should take

when pattern p_i matches a lexeme. Actions are written in C code.



User subroutinesare auxiliary procedures needed by the actions. These can be compiledseparately and loaded with the lexical analyzer.

YACC- YET ANOTHER COMPILER-COMPILER

Yacc provides a general tool for describing the input to a computer program. The Yacc user specifies the structures of his input, together with code to be invoked as each such structure is recognized.

Yacc turns such a specification into a subroutine that handles the input process; frequently, it is convenient and appropriate to have most of the flow of control in the user's application handled by this subroutine.

Finite Automata

Finite Automata is one of the mathematical models that consist of a number of states and edges. It is a transition diagram that recognizes a regular expression or grammar.

There are tow types of Finite Automata :

·                    Non-deterministic Finite Automata (NFA)

·                    Deterministic Finite Automata (DFA)

Deterministic Finite Automata

DFA is a special case of a NFA in which i) no state has an ε-transition.

ii)          there is at most one transition from each state on any input.

DFA has five tuples denoted by

M = {Q_d, Ʃ, δ, q₀, f_d}

Q_d – finite set of states

Ʃ            – finite set of input symbols

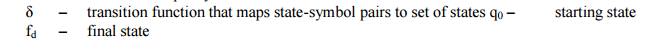
Construction of DFA from regular expression

The following steps are involved in the construction of DFA from regular expression:

Convert RE to NFA using Thomson’s rules

Convert NFA to DFA

Construct minimized DFA