Simplified Analysis of Curved Beams

Simplified Analysis of Curved Beams

As for straight beams, it is possible to develop a strength-of-materials-type solution for curved beams from the assumption that plane sections remain plain during flexure. We can then compare this Winkler solution* to the more accurate results from elasticity theory to see when added refinement is necessary.

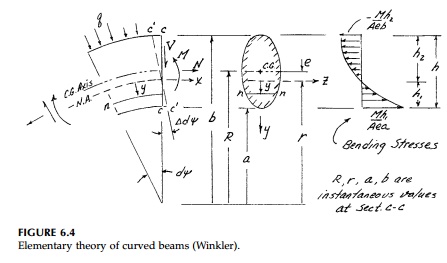
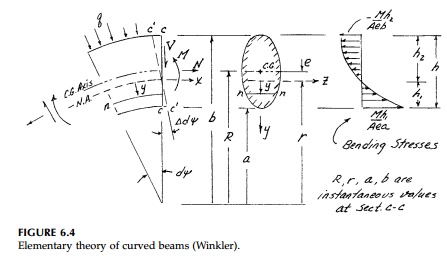
Consider a differential slice from a curved beam and call the tangent to the neutral axis at any cross-section x, the radial coordinate, y, positive inward as shown in Figure 6.4. Assume that:

a.  The transverse loading as well as the cross-section is symmetric and the bending moment is in the plane of symmetry (the xy plane).

b.  The radial stress is neglected.

c.  If there is shear and/or normal force on the cross-section they induce shear and/or normal stresses as in the elementary straight beam formulas.

d.   Transverse sections remain plane (i.e., plane câ€'c rotates around the z axis an angle Î'dΨ)

While these are the same assumptions used for the elementary analysis of straight beams, for a curved beam the longitudinal fibers are not all the same original base length. Therefore, linear displacements produce nonlinear strains. For a layer of longitudinal fibers nâ€'n, a distance y from the neutral axis at radius r, the rotation of the cross-section Î'dΨ due to M gives:

which is hyperbolic, not linear. For equilibrium, the neutral axis must be below the centroidal axis (radius R) such that:

Thus for a curved beam, the formulas for flexure with N and V by this Winkler analysis are:

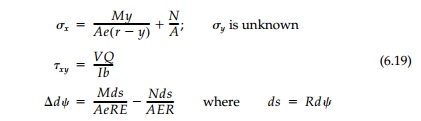
where e, the distance from the centroidal axis to the neutral axis, is a property of the cross-section such that (b) is satisfied. Formulas for various useful shapes are given in many books. For the rectangular cross-section of unit thickness necessary for comparison to an elasticity solution:

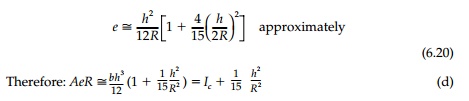
showing that only for very deep beams is there an appreciable increase in the flexural stiffness.