Airy’s Stress Function in Cartesian Coordinates

Airy’s Stress Function in Cartesian Coordinates

To review once again, the basic field equations in terms of stress are: Equilibrium:

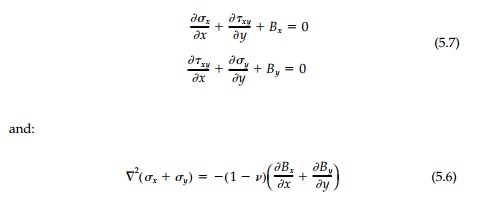
Once the stress field is determined, the elastic strains and rotations are found from the stress�'strain and conjugate relationships giving the components of the relative deformation vector du, dv, dw which can then be integrated for the displacement field.

In 1862, G.B. Airy introduced his potential function defined as:

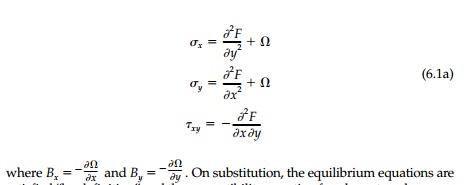
satisfied “by definition” and the compatibility equation for plane stress becomes

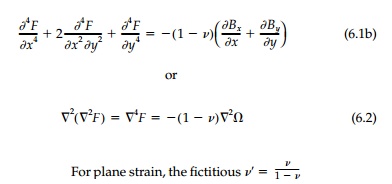
is substituted for v. If the body forces   are given by a harmonic function (e.g., constant, linear, magnetic fields, seep-age, etc.), Equation (6.2) reduces to the homogeneous elliptic form known as the biharmonic equation:

With this ingenious approach, Airy reduces the two-dimensional prob-lem to solving one equation.* Generally, if body forces are significant, their effect is solved for separately as in Chapter 5 and introduced by superposi-tion. Therefore, unless specifically stated to be otherwise, body forces will be neglected and Equation (6.3) used in this and succeeding pages.

The Classic Stress-Function Approach

Most solutions in two dimensions, for other than linear stress fields where direct integration is possible, can be obtained most easily by the semi-inverse method using stress functions. Usually Airy’s stress function is employed which, in two dimensions, reduces the three field equations to one fourth-order partial differential equation.* This “biharmonic equation” is exact for plane strain and nearly so for plane stress if the plate is reasonably thin.