Circular Beams with End Loads

Circular Beams with End Loads

Consider the semicircular beam of rectangular cross-section bent by radial loads P applied at either end as shown in Figure 6.7. The cross-section is rectangular of unit width and assume plane stress. The bending moment at any radial cut is PR sinθ and from the Winkler solution we would expect that  ÏƒÎ¸f(r)sinθ. Therefore from Section 6.4 we need a stress function of Type II with m = 1.

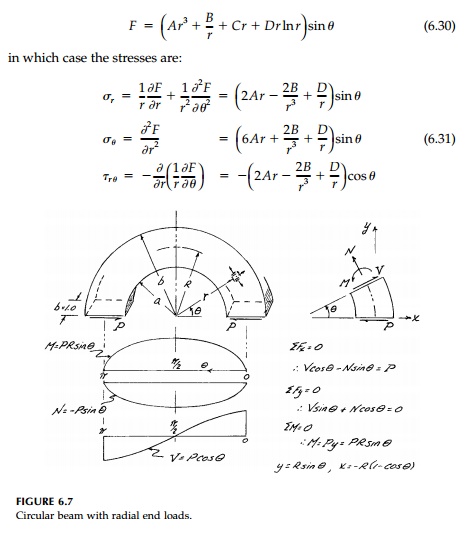
For this exact solution to apply at the ends of the beam, P must be distributed as dictated by the solution for Ï„_rθ at Î¸ = 0 and Ï€. If this is not the case, the solution will, by St. Venant’s principle, still apply at distances away from the end in the order of (bâ€'a).

Detailed comparison to the simpler Winkler solution [Equation (6.19)] is left to the chapter problems, but the agreement is again extremely close. The

The elastic rotation, Ï‰_z, satisfying Laplace’s equation can be found directly from the Cauchy-Riemann conditions. The first stress invariant is:

This is roughly the same relative difference as it was for pure bending.

The elastic displacement field can be determined by integrating the strains in the same way as was done for pure bending. Following this procedure:

where the constants H, K, and L are calculated from the geometric conditions associated with the supports. If we assume the centerline is pinned at

corresponding to elementary analysis. Further comparison of the deflections of thick rings is left to the solved problems, but again the results from elas-ticity and Winkler analysis are in close agreement.