Polar Coordinates and Airy’s Stress Function

Polar Coordinates and Airy’s Stress Function

The fundamental relationships for plane polar coordinates as given in next pages were obtained as a special case of general curvilinear coordinates. Since polar coordinates are so useful, let us re-derive them from basic principles. First con-sider equilibrium of a differential element as shown in Figure 6.3a.

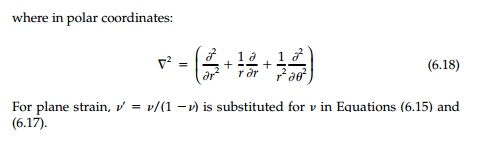
Thus, as with rectangular coordinates, there is the question of these equations not being satisfied for plane stress. Again we will assume loads are symmetric with z and we consider the plate to be thin enough to avoid any serious difficulties.

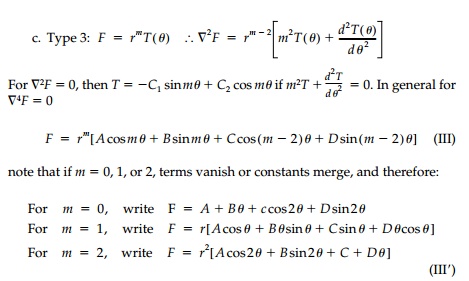
In every case there are four terms with unknown coefficients, A, B, C, and D to determine. The choice of which type of stress function and what terms to use will become apparent from considering the anticipated structural action, the boundary conditions available, and comparison to special cases approxi-mated by elementary analysis.

Example 6.2

The casement for a particle accelerator is a thick steel ring where the magnetic field introduces a body force in the radial direction, which dies off linearly with the radius as shown below.

Determine the elasticity solution. Assume plane strain and determine both the stress field and the displacements.