Chapter: Civil : Principles of Solid Mechanics : Two Dimensional Solutions for Straight and Circular Beams
Pure bending of a Beam of Circular Arc
Pure bending of
a Beam of Circular Arc
Consider a circular
beam of constant rectangular cross-section bent by end moments in the plane of
curvature (Figure 6.5). Since the moment diagram is con-stant, stresses are
only a function of r and a stress function of type I is called for:
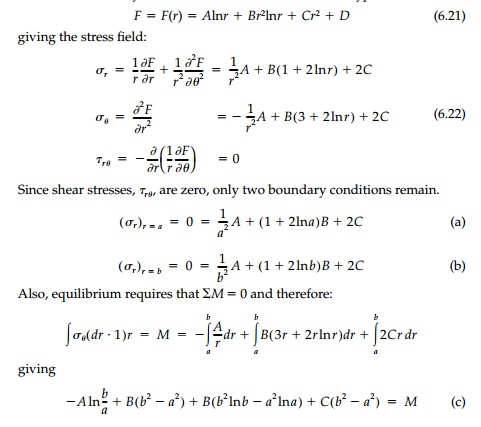




Equations (6.24) and
(6.25) can now be evaluated for the displacements since all the constants A,
B, C, D, F, H, and K are known.
The rotation and the
displacements for a particular beam can be computed from the Winkler and
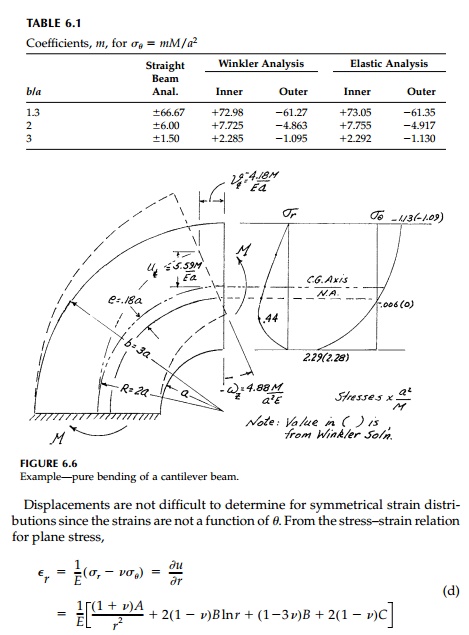
elasticity solutions for comparison. Results for a deep beam (Figure 6.6) are
presented in Table 6.2. The Winkler or elementary val-ues of the displacements
at the free end, θ = π/2, are computed by
integration

Comparing the two
solutions, we see that again, agreement is excellent. At the neutral axis, ur
is the same. The elasticity values are computed assuming v = 1/4
and therefore K = - 5.585 M/aE. If, instead v=0,
then K = - 5.78 M/aE and the agreement in vθ would essentially be exact. The discrepancy in vθ at the inner and outer fibers, which is still small, is due primarily to the
difference in the rotation that accumulates when integrated over the arc length
and is then multiplied by the distance from the neutral axis in computing the
longitudinal displacement.
Although the radial
displacement at the centerline depends slightly on Pois-son’s ratio due to the K
term, the small radial change in thickness:
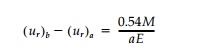
Thus, considering both
stresses and displacements, the close agreement of values computed from the
simple Winkler analysis indicates that the added refinement from elasticity
theory, while very satisfying, is of little practical significance.
Related Topics