Definition, Properties of Set Operations | Mathematics - Sets | 11th Mathematics : UNIT 1 : Sets, Relations and Functions
Chapter: 11th Mathematics : UNIT 1 : Sets, Relations and Functions
Sets
Sets
In the earlier
classes, we have seen that a set is a collection of well-defined objects. As the theory of sets
is the building blocks of modern mathematics, one has to learn the concepts of
sets carefully and deeply. Now we look at the term “well-defined” a little more
deeply. Consider the two statements:
i.
The collection of all beautiful flowers in Ooty Rose Garden.
ii.
The collection of all old men in Tamilnadu.
The terms “beautiful
flowers” and “old men” are not well-defined. We cannot define the term
“beautiful flower” in a sharp way as there is no concrete definition for beauty
because the concept of beauty varies from person to person, content to content
and object to object. We should not consider statements like “the collection of
all beautiful flowers in Ooty Rose Garden” as a set. Now, can we say “the
collection of all red flowers in Ooty Rose Garden” a set? The answer is “yes”.
One may consider a
person of age 60 as old and others may not agree. There is no specific and
concrete definition for “old men”. The second statement can be made more
sharply as “the collection of all men in Tamilnadu of age greater than 70”.
Now, the above
collection becomes a set because of definiteness in the age. Thus, the
description of a set should enable us to concretely decide whether a given
particular object (element) is available in the collection or not. So set is a
distinguishable collection of objects.
We have also seen and
learnt to use symbols like ∈, ⊂, ⊆, ∪ and ∩. Let us start with
the question:
“If A and B are two sets, is it
meaningful to write A ∈ B?”.
At the first sight one
may hurry to say that this is always meaningless by telling, “the symbol ∈ should be used between an element and a set and it should not
be used between two sets”. The first part of the statement is true whereas the
second part is not true. For example, if A = {1,
2}
and = {1, {1, 2}, 3, 4}, then A ∈
B. In this section we shall discuss the meaning
of such symbols more
deeply.
As we learnt in the
earlier classes the set containing no elements is called an empty set or a void set. It is usually
denoted by ∅ or { }. By A ⊆ B, we mean every element of the set A is an element of the set B. In this case, we say
A is a subset of B and B is a super set of A. For any two sets A and B , if A ⊆ B and B ⊆ A, then the two sets are equal. For any set A, the empty set ∅ and the set A are always subsets of A. These two subsets
are called trivial subsets. Further, we say A is a proper subset of B if A is a subset of B and A = B. That is, B contains all elements
of A and at least one element which is not in A. Note that, as every element of A is an element of A, we have A ⊆ A. Thus, any set is a
subset of itself. This subset is called an improper subset. In other words, for any set A, A is the improper
subset of A. It is known that, N ⊂ W ⊂ Z ⊂ Q ⊂ R, where N denotes the set of all natural numbers or positive integers, W denotes the set of all non-negative integers,
Z denotes the set of all integers, Q denotes the set of all rational numbers and R denotes the set of all real numbers. Note
that, the set of all irrational numbers is a subset of R but not a subset of any other set mentioned
above.
We learnt that the union of two sets A and B is denoted by A ∪ B and is defined as
A ∪ B = {x :
x ∈ A or x ∈ B}
and the intersection as
A ∩ B = {x :
x ∈ A and x ∈ B}.
Two sets A and B are disjoint if they do not have
any common element. That is, A and B are disjoint if A ∩ B = ∅.

Now, to define the
complement of a set, it is necessary to know about the concept of universal
set. Usually all sets under consideration in a mathematical process are assumed
to be subsets of some fixed set. This basic set is called the universal set. For example,
depending on the situation, for the set of prime numbers, the universal set can
be any one of the sets containing the set of prime numbers. Thus, one of the
sets N,
W,
Z,
Q,
R may be taken as a universal set for the set
of prime numbers, depending on the requirement. Universal set is usually
denoted by U.
To define the
complement of a set, we have to fix the universal set. Let A be a subset of the universal set U. The complement of A with respect to U is denoted as A or Ac and defined as A’ = {x :
x ∈ U and x ∈! A}.
The set difference of the set A to the set B is denoted by either A − B or A \ B and is defined as A − B = {a : a ∈ A and a ∈/ B}.
Note that,

Properties of Set Operations

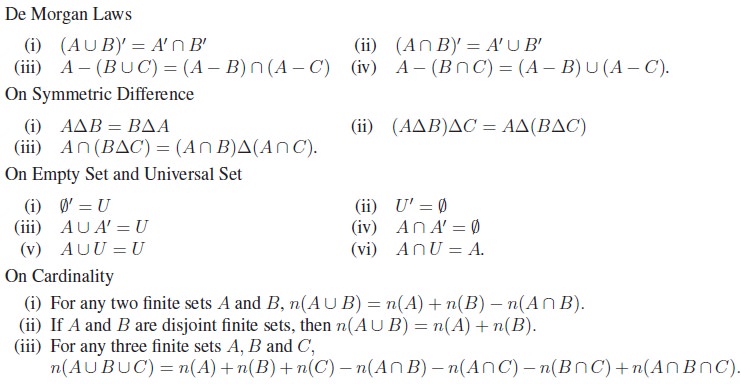
Related Topics