Sets, Relations and Functions | Mathematics - Exercise 1.5: Choose the correct or the most suitable answer | 11th Mathematics : UNIT 1 : Sets, Relations and Functions
Chapter: 11th Mathematics : UNIT 1 : Sets, Relations and Functions
Exercise 1.5: Choose the correct or the most suitable answer
CHAPTER: Sets, Relations and Functions
Choose the correct or the most suitable answer.
1. If A = {(x, y) : y = ex, x∈R} and B = {(x, y) : y = e-x, x ∈ R} then n(A ∩ B) is
(1) Infinity
(2) 0
(3) 1
(4) 2
Solution
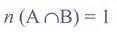
2. If A = {(x, y) : y = sin x, x ∈ R} and B = {(x, y) : y = cos x, x ∈ R} then A ∩ B contains
(1) no element
(2) infinitely many elements
(3) only one element
(4) cannot be determined.
3. The relation R defined on a set A = {0,-1, 1, 2} by xRy if |x2 + y2| ≤ 2, then which one of the following is true?
(1) R = {(0, 0), (0,-1), (0, 1), (-1, 0), (-1, 1), (1, 2), (1, 0)}
(2) R-1 = {(0, 0), (0,-1), (0, 1), (-1, 0), (1, 0)}
(3) Domain of R is {0,-1, 1, 2}
(4) Range of R is {0,-1, 1}
Solution
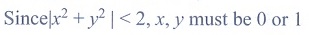
4. If {(x) = |x – 2| + |x + 2|, x ∊ R, then
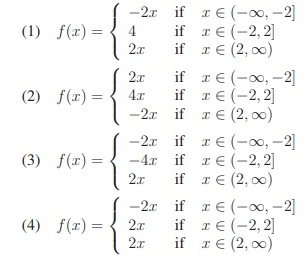
Ans: 1
Solution
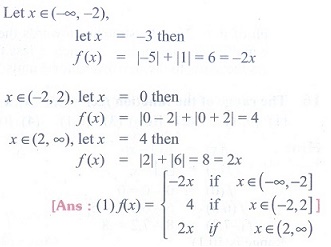
5. Let R be the set of all real numbers. Consider the following subsets of the plane R x R:
S = {(x, y) : y = x + 1 and 0 < x < 2} and T = {(x, y) : x - y is an integer }
Then which of the following is true?
(1) T is an equivalence relation but S is not an equivalence relation.
(2) Neither S nor T is an equivalence relation
(3) Both S and T are equivalence relation
(4) S is an equivalence relation but T is not an equivalence relation.

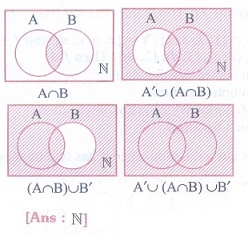
6. Let A and B be subsets of the universal set N, the set of natural numbers. Then A’∪ [(A∩B)∪B’] is
(1) A
(2) A’
(3) B
(4) N
Solution
7. The number of students who take both the subjects Mathematics and Chemistry is 70. This
represents 10% of the enrollment in Mathematics and 14% of the enrollment in Chemistry. The
number of students take at least one of these two subjects, is
(1) 1120
(2) 1130
(3) 1100
(4) insufficient data
Solution

8. If n((A x B) ∩ (A x C)) = 8 and n(B ∩ C) = 2, then n(A) is
(1) 6
(2) 4
(3) 8
(4) 16
Solution
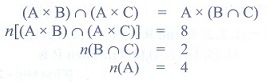
9. If n(A) = 2 and n(B ∪C) = 3, then n[(A x B) ∪ (A xC)] is
(1) 23
(2) 32
(3) 6
(4) 5
Solution
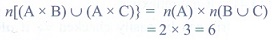
10. If two sets A and B have 17 elements in common, then the number of elements common to the
set A x B and B x A is
(1) 217
(2) 172
(3) 34
(4) insufficient data
Solution

11. For non-empty sets A and B, if A ⊂ B then (A x B) ∩ (B x A) is equal to
(1) A ∩ B
(2) A x A
(3) B x B
(4) none of these.
Solution
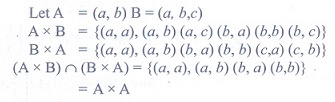
12. The number of relations on a set containing 3 elements is
(1) 9
(2) 81
(3) 512
(4) 1024
Solution
Let S = {a,b,c}
n(S) = 3
n(S x S) = 9
Number of relations in n{P(SxS)} = 29 = 512
13. Let R be the universal relation on a set X with more than one element. Then R is
(1) not reflexive
(2) not symmetric
(3) transitive
(4) none of the above
Solution
Let X ={a,b,c}
Then R = Universal relation
= {(a,a), (a,b)(a,c)(b,a), (b,b)(b,c)(c,a), (c,b)(c,c)}
14. Let X = {1, 2, 3, 4} and R = {(1, 1), (1, 2), (1, 3), (2, 2), (3, 3), (2, 1), (3, 1), (1, 4), (4, 1)}. Then
R is
(1) reflexive
(2) symmetric
(3) transitive
(4) equivalence
Solution

15. The range of the function 1 / 1-2 sin x is
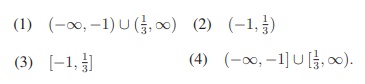
Ans: 4
Solution
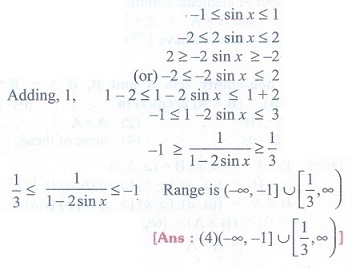
16. The range of the function f(x) = |└ x┘- x| , x ∊ R is
(1) [0, 1]
(2) [0, ∞)
(3) [0, 1)
(4) (0, 1)
Solution
17. The rule f(x) = x2 is a bijection if the domain and the co-domain are given by
(1) R,R
(2) R, (0, ∞)
(3) (0, ∞),R
(4) [0, ∞), [0, ∞)
Solution
18. The number of constant functions from a set containing m elements to a set containing n elements
is
(1) mn
(2) m
(3) n
(4) m + n
19. The function f : [0, 2π] → [-1, 1] defined by f(x) = sin x is
(1) one-to-one
(2) onto
(3) bijection
(4) cannot be defined
Solution

20. If the function f : [-3, 3] → S defined by f(x) = x2 is onto, then S is
(1) [-9, 9]
(2) R
(3) [-3, 3]
(4) [0, 9]
Solution

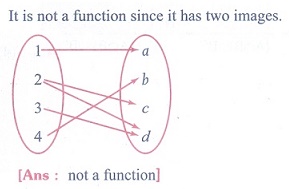
21. Let X = {1, 2, 3, 4}, Y = {a, b, c, d} and f = {(1, a), (4, b), (2, c), (3, d), (2, d)}. Then f is
(1) an one-to-one function
(2) an onto function
(3) a function which is not one-to-one
(4) not a function
Solution
22. The inverse of
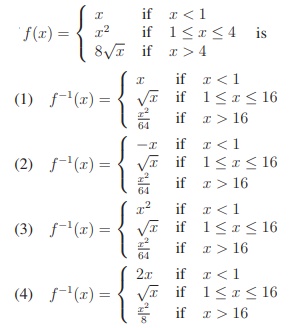
Ans: 1
Solution
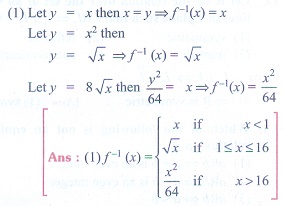
23. Let f : R → R be defined by f(x) = 1 - |x|. Then the range of f is
(1) R
(2) (1,∞)
(3) (-1, ∞)
(4) (-∞, 1]
Solution
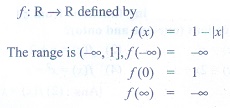
24. The function f : R → R is defined by f(x) = sin x + cos x is
(1) an odd function
(2) neither an odd function nor an even function
(3) an even function
(4) both odd function and even function.
Solution
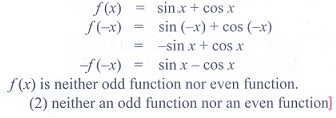
25. The function f : R → R is defined by
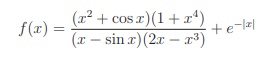
is
(1) an odd function
(2) neither an odd function nor an even function
(3) an even function
(4) both odd function and even function.
Solution
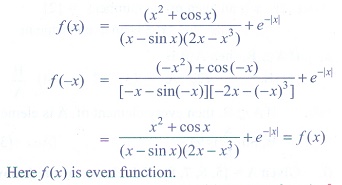
Related Topics