Mathematics - Constants and Variables, Intervals and Neighbourhoods | 11th Mathematics : UNIT 1 : Sets, Relations and Functions
Chapter: 11th Mathematics : UNIT 1 : Sets, Relations and Functions
Constants and Variables, Intervals and Neighbourhoods
Constants and Variables, Intervals and Neighbourhoods
To continue our discussion, we
need certain prerequisites namely, constants, variables, independent variables,
dependent variables, intervals and neighbourhoods.
1. Constants and Variables
A quantity that
remains unaltered throughout a mathematical process is called a constant. A quantity that
varies in a mathematical process is called a variable. A variable is an independent variable when it takes any arbitrary (independent)
value not depending on any other variables, whereas if its value depends on
other variables, then it is called a dependent variable.
We know the area A of a triangle is given by A = 1/2 bh. Here 1/2 is a constant and A, b, h are variables.
Moreover b and h are independent
variables and A is a dependent
variable. We ought to note that the terms dependent
and independent are relative terms.
For example in the equation x + y = 1, x, y are variables and 1 is a constant. Which of x and y is dependent and which
one is independent? If we consider x as an independent variable, then y becomes a dependent
whereas if we consider y as an independent
variable, then x becomes dependent.
Further consider the
following examples:
i.
area of a rectangle A = lb.
ii.
area of a circle A = πr2.
iii.
volume of a cuboid V = lbh.
From the above
examples we can directly infer that b, h, l , r are independent
variables; A and V are dependent
variables and π is a constant .
2. Intervals and Neighbourhoods
The system R of real numbers can be represented by the
points on a line and a point on the line can be related to a unique real number
as in Figure 1.2. By this, we mean that any real number can be identified as a
point on the line. With this identification we call the line as the real line.

The value increases as
we go right and decreases as we go left. If x lies to the left of y on the real line then x < y. As there is no gap
in a line, we have infinitely many real numbers between any two real numbers.

Note that the set of all natural
numbers, the set of all non-negative integers, set of all odd integers, set of
all even integers, set of all prime numbers are not intervals. Further observe
that, between any two real numbers there are infinitely many real numbers and
hence the above examples are not intervals.
Consider the following sets:
i.
The set of all real numbers greater than 0.
ii.
The set of all real numbers greater than 5 and less than 7.
iii.
The set of all real numbers x such that 1 ≤ x ≤ 3.
iv.
The set of all real numbers x such that 1 < x ≤ 2.
The above four sets are
intervals. In particular (i) is an infinite interval and (ii), (iii) and (iv)
are finite intervals. The term “finite interval” does not mean that the
interval contains only finitely many real numbers, however both ends are finite
numbers. Both finite and infinite intervals are infinite sets. The intervals
correspond to line segments are finite intervals whereas the intervals that
correspond to rays and the entire real line are infinite intervals.
A finite interval is
said to be closed if it contains both
of its end points and open if it contains neither of its end points. Symbolically the
above four intervals can be written as (0, ∞),
(5, 7), [1, 3], (1,
2]. Note that for
symbolic form we used parentheses and square brackets to denote intervals. ( ) parentheses indicate open interval and [ ] square brackets indicate closed interval. The
first two examples are open intervals, third one is a closed interval. Note
that fourth example is neither open nor closed, that is, one end open and other
end closed.
In particular [1,
3] contains both 1 and 3 and in between real
numbers. The interval (1, 3) does not contain 1 and 3 but contains all in
between the numbers. The interval (1, 2] does not contain 1 but contains 2 and all in between numbers.
Note that ∞ is not a number. The symbols −∞ and ∞ are used to indicate the ends of real line. Further, the
intervals (a, b) and [a, b] are subsets of R.
Type of Intervals
There are many types
of intervals. Let a, b ∈ R such that a < b. The following table describes various types of intervals. It
is not possible to draw a line if a point is removed. So we use an unfilled
circle “◦” to indicate that the point is removed and use a filled circle
“•” to indicate that the point is included.
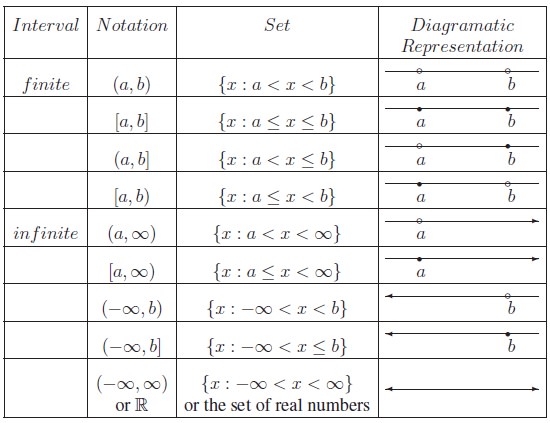
Try to write the following
intervals in symbolic form.

Neighbourhood
Neighbourhood of a point ‘a’ is any open interval containing ‘a’. In particular, if Î is a positive number, usually very small, then the Î-neighbourhood of ‘a’ is the open interval (a − Î, a + Î). The set (a −Î , a +Î ) − {a} is called deleted neighbourhood of ‘a’ and it is denoted as 0 < |x − a| < Î (See Figure 1.3).

Related Topics