Definition, Formula, Solved Example Problems, Exercise | Mathematics - Relations | 11th Mathematics : UNIT 1 : Sets, Relations and Functions
Chapter: 11th Mathematics : UNIT 1 : Sets, Relations and Functions
Relations
Relations
We approach the concept of relations in different aspects using real life sense, Cryptography and Geometry through Cartesian products of sets.
In our day to day life very often we come across questions like, “How is he related to you?”. Some probable answers are,
i. He is my father.
ii. He is my teacher.
iii. He is not related to me.
From this we see that the word relation connects a person with another person. Extending this idea, in mathematics we consider relations as one which connects mathematical objects. Examples,
i. A number m is related to a number n if m divides n in N.
ii. A real number x is related to a real number y if x ≤ y.
iii. A point p is related to a line L if p lies on L.
iv. A student X is related to a school S if X is a student of S.
Illustration 1.1 (Cryptography) For centuries, people have used ciphers or codes, to keep confi-dential information secure. Effective ciphers are essential to the military, to financial institutions and to computer programmers. The study of the techniques used in creating coding and decoding these ciphers is called cryptography.
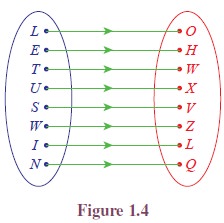
One of the earliest methods of coding a message was a simple substitution. For example, each letter in a message might be replaced by the letter that appears three places later in the alphabet.
Using this coding scheme, “LET US WIN” becomes “OHW XVZ LQ”. This scheme was used by Julius Caesar and is called the Caesars cipher. To decode, replace each letter by the letter three places before it. This concept is used often in Mental Ability Tests. The above can be represented as an arrow diagram as given in Figure 1.4.
This can be viewed as the set of ordered pairs
{(L, O), (E, H), (T, W ), (U, X), (S, V ), (W, Z), (I, L), (N, Q)}
which is a subset of the Cartesian product C × D where C = {L, E, T, U, S, W, I, N} and D = {O, H, W, X, V, Z, L, Q}.
Illustration 1.2 (Geometry) Consider the following three equations
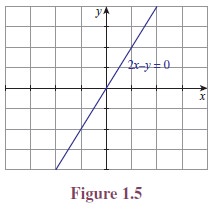
(i) 2x − y = 0
(ii) x2 − y = 0
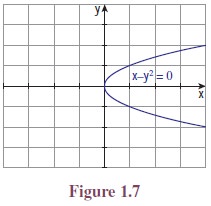
(iii) x − y2 = 0
(i) 2x − y = 0
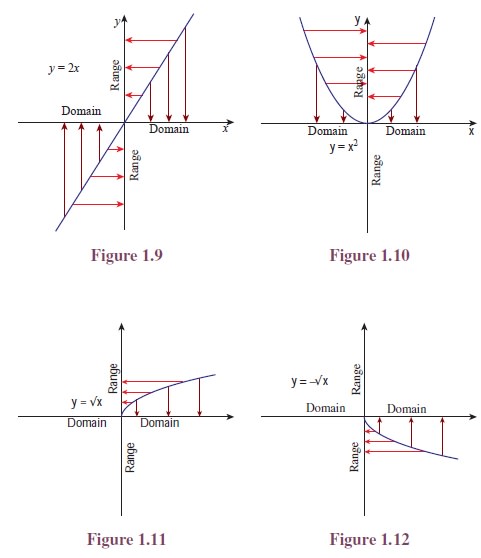
The equation 2x − y = 0 represents a straight line. Clearly the points, (1, 2), (3, 6) lie on it whereas (1, 1), (3, 5), (4, 5) are not lying on the straight line. The analytical relation between x and y is given by y = 2x. Here the values of y depends on the values of x. To denote this dependence, we write y = f(x). The set of all points that lie on the straight line is given as {(x, 2x) : x ∈ R}. Clearly this is a subset of R × R. (See Figure 1.5.)
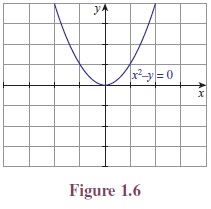
(ii) x2 − y = 0.
As we discussed earlier, the relation between x and y is y = x2. The set of all points on the curve is {(x, x2) : x ∈ R} (See Figure 1.6). Again this is a subset of the Cartesian product RxR.
(iii) x − y2 = 0

From the above examples we intuitively understand what a relation is. But in mathematics, we have to give a rigorous definition for each and every technical term we are using. Now let us start defining the term “relation” mathematically.
Definition of Relation
Let A = {p, q, r, s, t, u} be a set of students and let B = {X, Y, Z, W } be a set of schools. Let us consider the following “relation”.
A student a ∈ A is related to a school S ∈ B if “a” is studying or studied in the school S.
Let us assume that p studied in X and now studying in W , q studied in X and now studying in Y , r studied in X and W , and now studying in Z, s has been studying in X from the beginning, t studied in Z and now studying in no school, and u never studied in any of these four schools.
Though the relations are given explicitly, it is not possible to give a relation always in this way. So let us try some other representations for expressing the same relation:

Among these four representations of the relation, the third one seems to be more convenient and comfortable to deal with a relation in terms of sets.
The set given in the third representation is a subset of the Cartesian product A × B. In Illustrations 1.1 and 1.2 also, we arrived at subsets of a Cartesian product.

A relation from A to B is different from a relation from B to A.
The set {a ∈ A : (a, b) ∈ R for some b ∈ B} is called the domain of the relation.
The set {b ∈ B : (a, b) ∈ R for some a ∈ A} is called the range of the relation.
Thus the domain of the relation R is the set of all first coordinates of the ordered pairs and the range of the relation R is the set of all second coordinates of the ordered pairs.’
Illustration 1.3 Consider the diagram in Figure 1.8. Here the alphabets are mapped onto the natural numbers. A simple cipher is to assign a natural number to each alphabet. Here a is represented by 1, b is represented by 2, . . . , z is represented by 26. This correspondence can be written as the set

Now we recall that the relations discussed in Illustrations 1.1 and 1.2 also end up with subsets of the cartesian product of two sets. So the term relation used in all discussions we had so far, fits with the mathematical term relation defined in Definition 1.2.
The domain of the relation discussed in Illustration 1.1 is the set {L, E, T, U, S, W, I, N} and the range is {O, H, W, X, V, Z, L, Q}. In Illustration 1.2, the domain and range of the relation discussed for the equation 2x − y = 0 are R and R (See Figure 1.9); for the equation x2 − y = 0, the domain is R and the range is [0, ∞) (See Figure 1.10); and in the case of the third equation x − y2 = 0, the domain is [0, ∞) and the range is R (See Figures 1.11 and 1.12).
Note that, the domain of a relation is a subset of the first set in the Cartesian product and the range is a subset of second set. Usually we call the second set as co-domain of the relation. Thus, the range of a relation is the collection of all elements in the co-domain which are related to some element in the domain. Let us note that the range of a relation is a subset of the co-domain.
For any set A, ∅ and A × A are subsets of A × A. These two relations are called extreme relations.
The former relation is an empty relation and the later is an universal relation.
We will discuss more about domain, co-domain and the range in the next section namely, “Functions”.
If R is a relation from A to B and if (x, y) ∈ R, then sometimes we write xRy (read this as “x is related to y”) and if (x, y) ∈/ R, then sometimes we write xRy (read this as “x is not related to y”).
Though the general definition of a relation is defined from one set to another set, relations defined on a set are of more interest in mathematical point of view. That is, relations in which the domain and the co-domain are the same are of more interest. So let us concentrate on relations defined on a set.
1. Type of Relations
Consider the following examples:
i. Let S = {1, 2, 3, 4} and R = {(1, 1), (1, 3), (2, 3)} on S.
ii. Let S = {1, 2, 3, . . . 10} and define “m is related to n, if m divides n”.
iii. Let C be the set of all circles in a plane and define “a circle C is related to a circle C , if the radius of C is equal to the radius of C ”.
iv. In the set S of all people define “a is related to b, if a is a brother of b”.
v. Let S be the set of all people. Define the relation on S by the rule “mother of”.
In the second example, as every number divides itself, “a is related a for all a ∈ S”; the same is true in the third relation also. In the first example “a is related a for all a ∈ S” is not true as 2 is not related to 2.
It is easy to see that the property “if a is related to b, then b is related to a” is true in the third but not in the second.
It is easy to see that the property “if a is related to b and b is related to c, then a is related to c” is true in the second and third relations but not in the fifth.
These properties, together with some more properties are very much studied in mathematical structures. Let us define them now.

Let us rewrite the definitions of these basic relations in a different form:
Let S be any non-empty set. Let R be a relation on S. Then R is
· reflexive if “(a, a) ∈ R for all a ∈ S”.
· symmetric if “(a, b) ∈ R ⇒ (b, a) ∈ R”.
· transitive if “(a, b), (b, c) ∈ R ⇒ (a, c) ∈ R”.
Let us consider the following two relations.
· In the set S1 of all people, define a relation R1 by the rule: “a is related to b, if a is a brother of b”.
· In the set S2 of all males, define a relation R2 by the rule: “a is related to b, if a is a brother of b”.
The rules that define the relations on S1 and S2 are the same. But the sets are not same. R1 is not a symmetric relation on S1 whereas R2 is a symmetric relation on S2. This shows that not only the rule defining the relation is important, the set on which the relation is defined, is also important. So whenever one considers a relation, both the relation as well as the set on which the relation is defined have to be given explicitly. Note that the relation {(1, 1), (2, 2), (3, 3), (1, 2)} is reflexive if it is defined on the set {1, 2, 3}; it is not reflexive if it is defined on the set {1, 2, 3, 4}.
Illustration 1.4
1. Let X = {1, 2, 3, 4} and R = {(1, 1), (2, 1), (2, 2), (3, 3), (1, 3), (4, 4), (1, 2), (3, 1)}. As (1, 1), (2, 2), (3, 3) and (4, 4) are all in R, it is reflexive. Also for each pair (a, b) ∈ R the pair (b, a) is also in R. So R is symmetric. As (2, 1), (1, 3) ∈ R and (2, 3) ∈/ R, we see that R is not transitive. Thus R is not an equivalence relation.
2. Let P denote the set of all straight lines in a plane. Let R be the relation defined on P as Rm if is parallel to m.
This relation is reflexive, symmetric and transitive. Thus it is an equivalence relation.
3. Let A be the set consisting of children and elders of a family. Let R be the relation defined by aRb if a is a sister of b.
This relation is to be looked into carefully. A woman is not a sister of herself. So it is not reflexive. It is not symmetric also. Clearly it is not transitive. So it is not an equivalence relation. (If we consider the same relation on a set consisting only of females, then it becomes symmetric; even in this case it is not transitive).
4. On the set of natural numbers let R be the relation defined by xRy if x + 2y = 21. It is better to write the relation explicitly. The relation R is the set
{(1, 10), (3, 9), (5, 8), (7, 7), (9, 6), (11, 5), (13, 4), (15, 3), (17, 2), (19, 1)}.
As (1, 1) ∈/ R it is not reflexive; as (1, 10) ∈ R and (10, 1) ∈/ R it is not symmetric.
As (3, 9) ∈ R, (9, 6) ∈ R but (3, 6) ∈/ R, the relation is not transitive.
5. Let X = {1, 2, 3, 4} and R = ∅, where ∅ is the empty set.
As (1, 1) ∈/ R it is not reflexive. As we cannot find a pair (x, y) in R such that (y, x) ∈/ R, the relation is not ‘not symmetric’; so it is symmetric. Similarly it is transitive.
6. The universal relation is always an equivalence relation.
7. An empty relation can be considered as symmetric and transitive.
8. If a relation contains a single element, then the relation is transitive.
Let us discuss some more special relations now.

From the very beginning we have denoted all the relations by the same letter R. It is not necessary to do so. We may use the Greek letter ρ (Read as rho) to denote relations. Equivalence relations are mostly denoted by “∼”.
If a relation is not of required type, then by inserting or deleting some pairs we can make it of the required type. We do this in the following problem.




Theorem 1.1: The number of relations from a set containing m elements to a set containing n elements is 2mn. In particular the number of relations on a set containing n elements is ![]()


For example, if R = {(1, a), (2, b), (2, c), (3, a)}, then
R−1 = {(a, 1), (b, 2), (c, 2), (a, 3)}.
It is easy to see that the domain of R becomes the range of R−1 and the range of R becomes the domain of R−1.


Related Topics