Definition, Formula, Solved Example Problems, Exercise | Mathematics - Graphing Functions using Transformations | 11th Mathematics : UNIT 1 : Sets, Relations and Functions
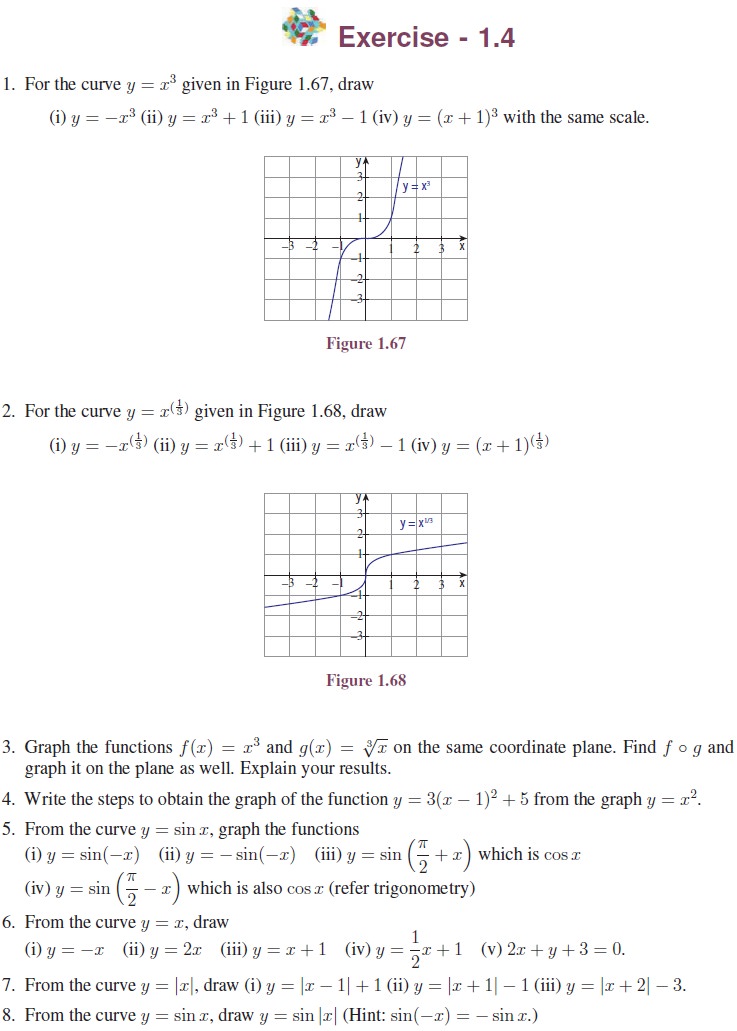
Chapter: 11th Mathematics : UNIT 1 : Sets, Relations and Functions
Graphing Functions using Transformations
Graphing Functions using Transformations
“A picture is worth a thousand words” is a well known proverb. To
know about a function well, its graph will help us more than its analytical
expression. To draw graphs quickly without plotting many points is an
invaluable skill. Familiarity with shapes of some basic functions will help to
graph other complicated functions. Understanding and usage of symmetry and
transformations will then enable to strengthen graphing abilities. This section
is not simply a data base of graphs, we learn some methods to graph certain
functions.
Suppose that we want
to draw or sketch the curve of the function y = 2 sin(x
− 1)
+ 3. At the very first
sight it looks that it is very difficult to draw the curve representing this
function. But it will be very easy to draw after understanding the content of
this section.
If we know a half of a
graph is the mirror image of the other half with respective to a line, or a
graph can be obtained just by moving a known graph in some direction, then we
can draw the new one using the known one. Moreover if we know that a graph can
be obtained by enlarging or shrinking a known one, then also we can draw the
new one using the known ones.
The following type of
transformations play very important roles in graphing.
i.
Reflection
ii.
Translation
iii.
Dilations.
In the case of
reflections and translations, they produce graphs congruent to the original
graph; that is, the size and the shape of the graph does not change, but in
dilation, it produce graphs with shapes related to those of the original graph.
Reflection
The reflection of the graph of a function with respect to a line is
the graph that is symmetric to it with respect to . A reflection is the mirror
image of the graph where line is the mirror of the reflection. (See Figure
1.47.)

Here f ‘ is the mirror image of f with respect to . Every point of
f has a corresponding image in f’ . Some useful reflections of y = f(x) are
i.
The graph y = −f(x)
is the reflection of the graph of f about the x-axis.
ii.
The graph y = f(−x) is the reflection of the graph of f about the y-axis.
iii.
The graph of y = f−1(x)
is the reflection of the graph of f in y = x.
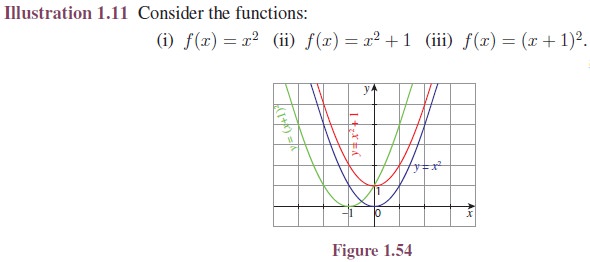
Illustration
1.5 Consider the functions:
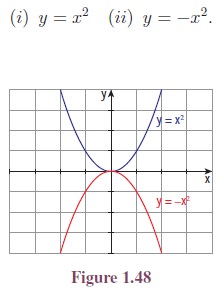
For the curve f(x) = x2, −f(x) = −x2. Hence, y = −x2 is the reflection of y = x2 about x-axis. (See Figure 1.48.)
Illustration 1.6 Consider the positive
branches of
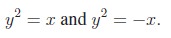
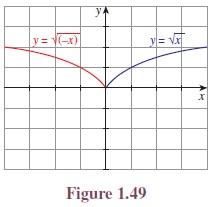
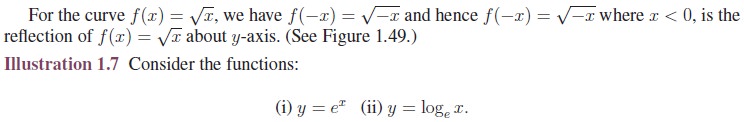
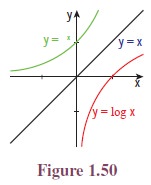
We know that, y = ex is the inverse function of y =
loge x and hence y = ex is the reflection of
= loge x about y = x. (See Figure 1.50.)
Translation
A translation of a
graph is a vertical or horizontal shift of the graph that produces congruent
graphs.
The graph of
y = f(x + c),c> 0
causes the shift to the left.
y = f(x − c),c> 0
causes the shift to the right.
y = f(x) + d, d > 0
causes the shift to the upward.
y = f(x) − d, d > 0
causes the shift to the downward.
Illustration 1.8 Consider the functions:
f(x) = |x| (ii) f(x) =
|x − 1| (iii) f(x) = |x + 1|
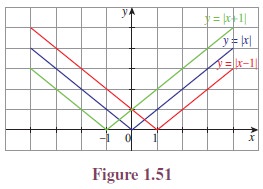
f(x) = |x − 1| causes
the graph of the function f(x) = |x| shifts to the right for one unit.
f(x) = |x + 1| causes
the graph of the function f(x) = |x| shifts to the left for one unit.
(See Figure 1.51.)
Illustration 1.9 Consider the functions:
(i) f(x) = |x| (ii)
f(x) = |x| − 1 (iii) f(x) = |x| + 1

f(x) =
|x| − 1 causes the graph of
the functionf(x) = |x| shifts to the downward
for one unit.
f(x) =
|x| + 1 causes the graph of
the function f(x) = |x| shifts to the upward
for one unit. (See Figure 1.52.)
Dilation
Dilation is also a transformation which
causes the curve stretches (expands) or compresses (con-tracts). Multiplying a
function by a positive constant vertically stretches or compresses its graph;
that is, the graph moves away from x-axis or towards x-axis.
If the positive constant is
greater than one, the graph moves away from the x-axis. If the positive constant
is less than one, the graph moves towards the x-axis.
Illustration
1.10
Consider the functions:
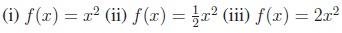
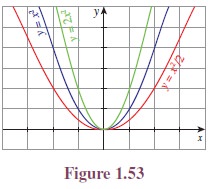

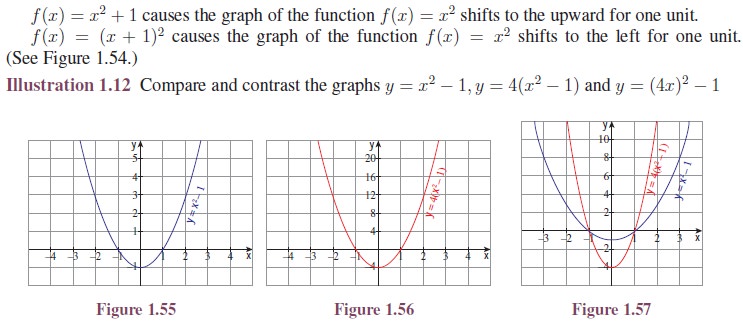
The graphs Figures
1.55 and 1.56 look identical until we compare the scales on the y-axis. The scale in Figure 1.56 is four times as large,
reflecting the multiplication of the original function by 4 (Figure 1.55). The effect looks different when
the functions are plotted on the same scale as in Figure 1.57.
The graph of y =
(4x)2 − 1 is shown in Figure
1.58. Can you spot the difference between Figure 1.55 and Figure 1.58? In this
case, x-scale has now changed, by the same factor of 4 as in the function (Figure 1.58). To see
this, note that substituting x = 1/4 into (4x)2 − 1 produces 12 − 1, exactly the same as
substituting x = 1 into the original function (Figure 1.55).
When plotted on the same set of axes (as in Figure 1.59) the parabola y =
(4x)2 − 1 looks thinner. Here,
the x-intercepts are different, but y-intercepts are the
same.
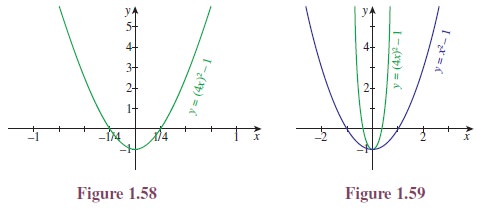
Illustration 1.13 By using the same
concept applied in Illustration 1.12, graphs of y = sin x and y= sin 2x, and also their
combined graphs are given Figures 1.60, 1.61 and 1.62. The minimum and maximum values of sin x and sin 2x
are the same. But they have different x-intercepts. The x-intercepts for y = sin x are ±nπ and for y =
sin 2x are ±1/2 nπ, n ∈ Z.

In the beginning of
the section we talked about drawing the graph of y = 2 sin(x
− 1)
+ 3. Now we are well
equipped to draw the curve and even we can draw more complicated curve.
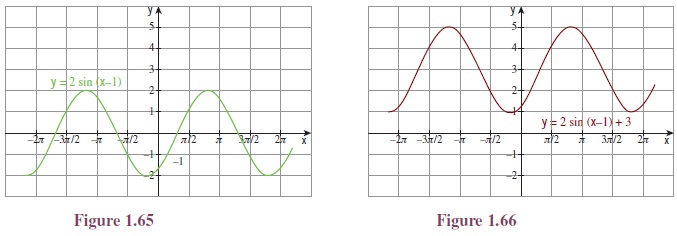
Illustration 1.14 Let us now draw the
graph of y = 2 sin(x − 1) + 3.
It is clear that the
curve can be obtained from that of y = sin x using translation and dilation.
So first we draw y =
sin x. From that it is easy to draw the curve y =
sin(x − 1); then draw y = 2 sin(x − 1) and finally y =
2 sin(x − 1) + 3. (See Figures 1.63 to
1.66.)

Related Topics