Definition, Formula, Solved Example Problems, Exercise | Mathematics - Cartesian Product | 11th Mathematics : UNIT 1 : Sets, Relations and Functions
Chapter: 11th Mathematics : UNIT 1 : Sets, Relations and Functions
Cartesian Product
In particular, Cartesian product of two sets is a set of ordered pairs, while the Cartesian product of three sets is a set of ordered triplets. Precisely, let A, B and C be three non-empty sets.
Cartesian Product
We know that the
Cartesian product of sets is nothing but a set of ordered elements. In
particular, Cartesian product of two sets is a set of ordered pairs, while the
Cartesian product of three sets is a set of ordered triplets. Precisely, let A, B and C be three non-empty
sets. Then the Cartesian product of A with B is denoted by A × B. It is defined by
Here A × B is a subset of R × R.
The number of elements in A × B is the product of the
number of elements in A and the number of
elements in B, that is, n(A × B)
= n(A)n(B), if A and B are finite. Further n(A
× B × C) = n(A)n(B)n(C),
if A, B and C are finite.
It is easy to see that
the following are the subsets of R × R.
Tags : Definition, Formula, Solved Example Problems, Exercise | Mathematics , 11th Mathematics : UNIT 1 : Sets, Relations and Functions
Study Material, Lecturing Notes, Assignment, Reference, Wiki description explanation, brief detail
11th Mathematics : UNIT 1 : Sets, Relations and Functions : Cartesian Product | Definition, Formula, Solved Example Problems, Exercise | Mathematics
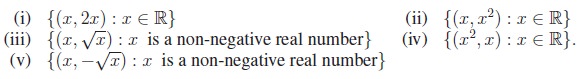
Related Topics
11th Mathematics : UNIT 1 : Sets, Relations and Functions