Search Trees and B-Trees

Search Trees and B-Trees

A search tree is a special type of tree that is used to guide the search for a record, given the value of one of the record’s fields. The multilevel indexes discussed in Section 18.2 can be thought of as a variation of a search tree; each node in the multilevel index can have as many as fo pointers and fo key values, where fo is the index fan-out. The index field values in each node guide us to the next node, until we reach the data file block that contains the required records. By following a pointer, we restrict our search at each level to a subtree of the search tree and ignore all nodes not in this subtree.

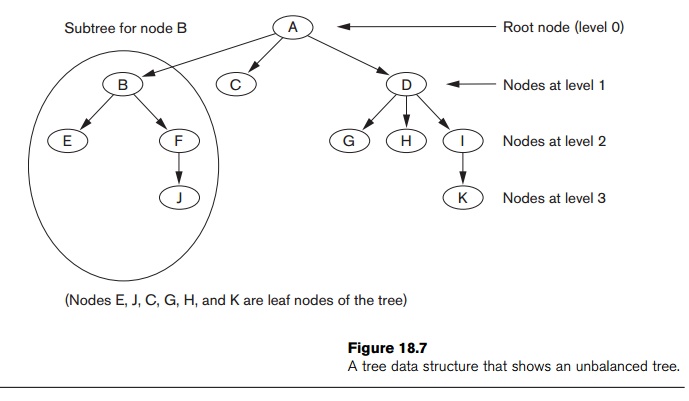
Search Trees. A search tree is slightly different from a multilevel index. A search tree of order p is a tree such that each node contains at most p − 1 search values and p pointers in the order <P1, K1, P2, K2, ..., Pq−1, Kq−1, Pq>, where q ≤ p. Each Pi is a pointer to a child node (or a NULL pointer), and each Ki is a search value from some ordered set of values. All search values are assumed to be unique.6 Figure 18.8 illustrates a node in a search tree. Two constraints must hold at all times on the search tree:

        Within each node, K1 < K2 < ... < Kq−1.

        For all values X in the subtree pointed at by Pi, we have Ki−1 < X < Ki for 1 <

i < q; X < Ki for i = 1; and Ki−1 < X for i = q (see Figure 18.8).

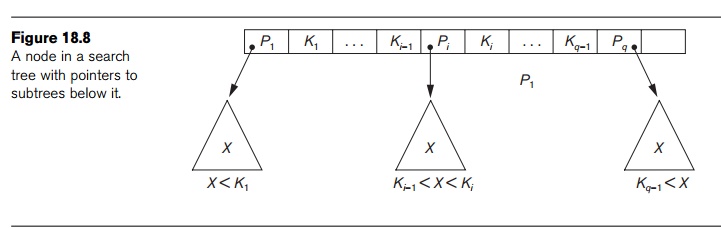
Whenever we search for a value X, we follow the appropriate pointer Pi according to the formulas in condition 2 above. Figure 18.9 illustrates a search tree of order p = 3 and integer search values. Notice that some of the pointers Pi in a node may be NULL pointers.

We can use a search tree as a mechanism to search for records stored in a disk file. The values in the tree can be the values of one of the fields of the file, called the search field (which is the same as the index field if a multilevel index guides the search). Each key value in the tree is associated with a pointer to the record in the data file having that value. Alternatively, the pointer could be to the disk block containing that record. The search tree itself can be stored on disk by assigning each tree node to a disk block. When a new record is inserted in the file, we must update the search tree by inserting an entry in the tree containing the search field value of the new record and a pointer to the new record.

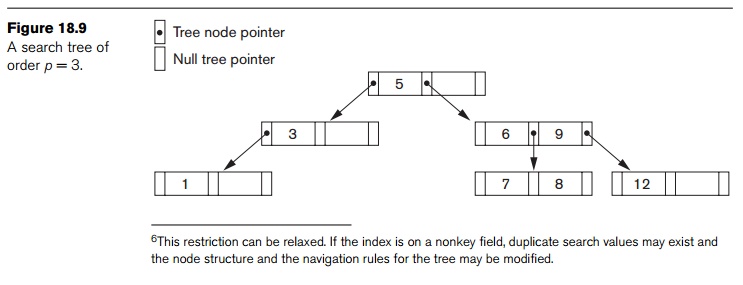
Algorithms are necessary for inserting and deleting search values into and from the search tree while maintaining the preceding two constraints. In general, these algorithms do not guarantee that a search tree is balanced, meaning that all of its leaf nodes are at the same level. The tree in Figure 18.7 is not balanced because it has leaf nodes at levels 1, 2, and 3. The goals for balancing a search tree are as follows:

                                 To guarantee that nodes are evenly distributed, so that the depth of the tree is minimized for the given set of keys and that the tree does not get skewed with some nodes being at very deep levels

                                         To make the search speed uniform, so that the average time to find any random key is roughly the same

While minimizing the number of levels in the tree is one goal, another implicit goal is to make sure that the index tree does not need too much restructuring as records are inserted into and deleted from the main file. Thus we want the nodes to be as full as possible and do not want any nodes to be empty if there are too many deletions. Record deletion may leave some nodes in the tree nearly empty, thus wasting storage space and increasing the number of levels. The B-tree addresses both of these problems by specifying additional constraints on the search tree.

B-Trees. The B-tree has additional constraints that ensure that the tree is always balanced and that the space wasted by deletion, if any, never becomes excessive. The algorithms for insertion and deletion, though, become more complex in order to maintain these constraints. Nonetheless, most insertions and deletions are simple processes; they become complicated only under special circumstances—namely, whenever we attempt an insertion into a node that is already full or a deletion from a node that makes it less than half full. More formally, a B-tree of order p, when used as an access structure on a key field to search for records in a data file, can be defined as follows:

1. Each internal node in the B-tree (Figure 18.10(a)) is of the form

<P1, <K1, Pr1>, P2, <K2, Pr2>, ..., <Kq–1, Prq–1>, Pq>

where q ≤ p. Each Pi is a tree pointer—a pointer to another node in the B-tree. Each Pri is a data pointer8—a pointer to the record whose search key field value is equal to Ki (or to the data file block containing that record).

   2. Within each node, K1 < K2 < ... < Kq−1.

        3. For all search key field values X in the subtree pointed at by Pi (the ith sub-tree, see Figure 18.10(a)), we have:

Ki–1 < X < Ki for 1 < i < q; X < Ki for i = 1; and Ki–1 < X for i = q. 

  4. Each node has at most p tree pointers.

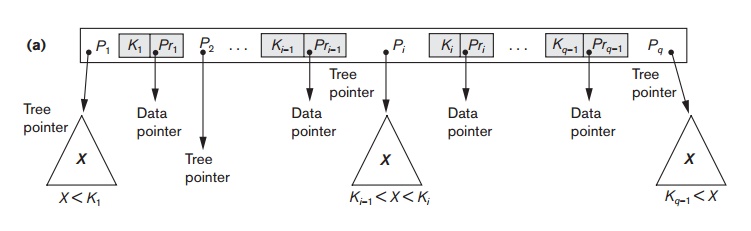
        5. Each node, except the root and leaf nodes, has at least (p/2) tree pointers. The root node has at least two tree pointers unless it is the only node in the tree.

        6. A node with q tree pointers, q ≤ p, has q – 1 search key field values (and hence has q – 1 data pointers).

        7. All leaf nodes are at the same level. Leaf nodes have the same structure as internal nodes except that all of their tree pointers Pi are NULL.

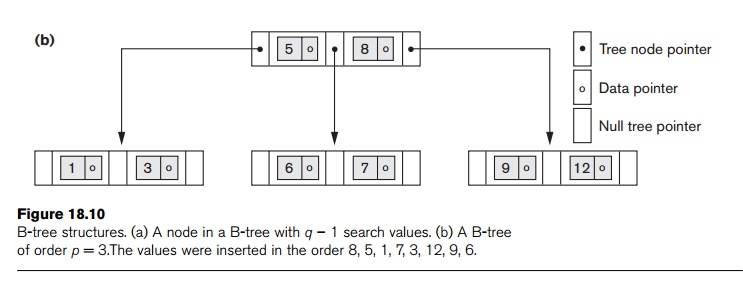
Figure 18.10(b) illustrates a B-tree of order p = 3. Notice that all search values K in the B-tree are unique because we assumed that the tree is used as an access structure on a key field. If we use a B-tree on a nonkey field, we must change the definition of the file pointers Pri to point to a block—or a cluster of blocks—that contain the pointers to the file records. This extra level of indirection is similar to option 3, dis-cussed in Section 18.1.3, for secondary indexes.

 A B-tree starts with a single root node (which is also a leaf node) at level 0 (zero). Once the root node is full with p – 1 search key values and we attempt to insert another entry in the tree, the root node splits into two nodes at level 1. Only the middle value is kept in the root node, and the rest of the values are split evenly between the other two nodes. When a nonroot node is full and a new entry is inserted into it, that node is split into two nodes at the same level, and the middle entry is moved to the parent node along with two pointers to the new split nodes. If the parent node is full, it is also split. Splitting can propagate all the way to the root node, creating a new level if the root is split. We do not discuss algorithms for B-trees in detail in this book,9 but we outline search and insertion procedures for B+-trees in the next section.

If deletion of a value causes a node to be less than half full, it is combined with its neighboring nodes, and this can also propagate all the way to the root. Hence, deletion can reduce the number of tree levels. It has been shown by analysis and simulation that, after numerous random insertions and deletions on a B-tree, the nodes are approximately 69 percent full when the number of values in the tree stabilizes. This is also true of B+-trees. If this happens, node splitting and combining will occur only rarely, so insertion and deletion become quite efficient. If the number of values grows, the tree will expand without a problem—although splitting of nodes may occur, so some insertions will take more time. Each B-tree node can have at most p tree pointers, p – 1 data pointers, and p – 1 search key field values (see Figure 18.10(a)).

In general, a B-tree node may contain additional information needed by the algorithms that manipulate the tree, such as the number of entries q in the node and a pointer to the parent node. Next, we illustrate how to calculate the number of blocks and levels for a B-tree.

Example 4. Suppose that the search field is a nonordering key field, and we con-struct a B-tree on this field with p = 23. Assume that each node of the B-tree is 69 percent full. Each node, on the average, will have p * 0.69 = 23 * 0.69 or approximately 16 pointers and, hence, 15 search key field values. The average fan-out fo = 16. We can start at the root and see how many values and pointers can exist, on the average, at each subsequent level:

Root: 1 node         15 key entries       16 pointers

Level 1:       16 nodes     240 key entries     256 pointers

Level 2:       256 nodes   3840 key entries   4096 pointers

Level 3:       4096 nodes 61,440 key entries        

At each level, we calculated the number of key entries by multiplying the total number of pointers at the previous level by 15, the average number of entries in each node. Hence, for the given block size, pointer size, and search key field size, a two-level B-tree holds 3840 + 240 + 15 = 4095 entries on the average; a three-level B-tree holds 65,535 entries on the average.

B-trees are sometimes used as primary file organizations. In this case, whole records are stored within the B-tree nodes rather than just the <search key, record pointer> entries. This works well for files with a relatively small number of records and a small record size. Otherwise, the fan-out and the number of levels become too great to permit efficient access.

In summary, B-trees provide a multilevel access structure that is a balanced tree structure in which each node is at least half full. Each node in a B-tree of order p can have at most p − 1 search values.