B+-Trees

B+-Trees

Most implementations of a dynamic multilevel index use a variation of the B-tree data structure called a B+-tree. In a B-tree, every value of the search field appears once at some level in the tree, along with a data pointer. In a B+-tree, data pointers are stored only at the leaf nodes of the tree; hence, the structure of leaf nodes differs from the structure of internal nodes. The leaf nodes have an entry for every value of the search field, along with a data pointer to the record (or to the block that contains this record) if the search field is a key field. For a nonkey search field, the pointer points to a block containing pointers to the data file records, creating an extra level of indirection.

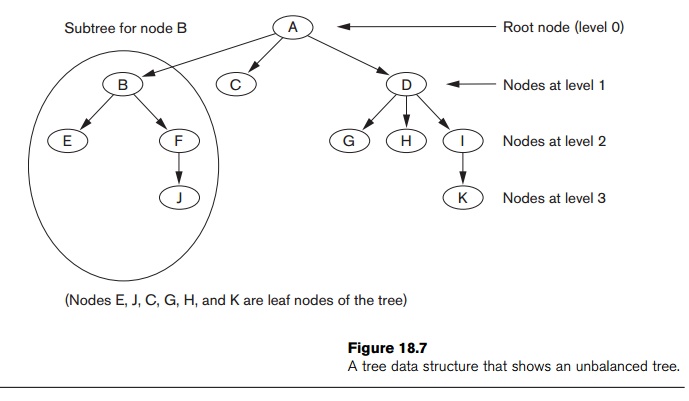
The leaf nodes of the B+-tree are usually linked to provide ordered access on the search field to the records. These leaf nodes are similar to the first (base) level of an index. Internal nodes of the B+-tree correspond to the other levels of a multilevel index. Some search field values from the leaf nodes are repeated in the internal nodes of the B+-tree to guide the search. The structure of the internal nodes of a B+-tree of order p (Figure 18.11(a)) is as follows:

1. Each internal node is of the form

<P1, K1, P2, K2, ..., Pq – 1, Kq –1, Pq> where q ≤ p and each Pi is a tree pointer.

        Within each internal node, K1 < K2 < ... < Kq−1.

        For all search field values X in the subtree pointed at by Pi, we have Ki−1 < X ≤ Ki for 1 < i < q; X ≤ Ki for i = 1; and Ki−1 < X for i = q (see Figure 18.11(a)).10

        Each internal node has at most p tree pointers.

        Each internal node, except the root, has at least (p/2) tree pointers. The root node has at least two tree pointers if it is an internal node.

        An internal node with q pointers, q ≤ p, has q − 1 search field values.

The structure of the leaf nodes of a B+-tree of order p (Figure 18.11(b)) is as follows:

1. Each leaf node is of the form

<<K1, Pr1>, <K2, Pr2>, ..., <Kq–1, Prq–1>, Pnext>

where q ≤ p, each Pri is a data pointer, and Pnext points to the next leaf node of the B+-tree.

        2. Within each leaf node, K1 ≤ K2 ... , Kq−1, q ≤ p.

        3. Each Pri is a data pointer that points to the record whose search field value is Ki or to a file block containing the record (or to a block of record pointers that point to records whose search field value is Ki if the search field is not a key).

        4. Each leaf node has at least  (p/2)  values.

        5. All leaf nodes are at the same level.

The pointers in internal nodes are tree pointers to blocks that are tree nodes, whereas the pointers in leaf nodes are data pointers to the data file records or blocks—except for the Pnext pointer, which is a tree pointer to the next leaf node. By starting at the leftmost leaf node, it is possible to traverse leaf nodes as a linked list, using the Pnext pointers. This provides ordered access to the data records on the indexing field. A Pprevious pointer can also be included. For a B+-tree on a nonkey field, an extra level of indirection is needed similar to the one shown in Figure 18.5, so the Pr pointers

are block pointers to blocks that contain a set of record pointers to the actual records in the data file, as discussed in option 3 of Section 18.1.3.

Because entries in the internal nodes of a B+-tree include search values and tree pointers without any data pointers, more entries can be packed into an internal node of a B+-tree than for a similar B-tree. Thus, for the same block (node) size, the order p will be larger for the B+-tree than for the B-tree, as we illustrate in Example 5. This can lead to fewer B+-tree levels, improving search time. Because the structures for internal and for leaf nodes of a B+-tree are different, the order p can be different. We will use p to denote the order for internal nodes and pleaf to denote the order for leaf nodes, which we define as being the maximum number of data pointers in a leaf node.

Example 5. To calculate the order p of a B+-tree, suppose that the search key field is V = 9 bytes long, the block size is B = 512 bytes, a record pointer is Pr = 7 bytes, and a block pointer is P = 6 bytes. An internal node of the B+-tree can have up to p tree pointers and p – 1 search field values; these must fit into a single block. Hence, we have:

(p * P) + ((p – 1) * V) ≤ B (P * 6) + ((P − 1) * 9) ≤ 512 (15 * p) ≤ 521

We can choose p to be the largest value satisfying the above inequality, which gives p = 34. This is larger than the value of 23 for the B-tree (it is left to the reader to compute the order of the B-tree assuming same size pointers), resulting in a larger fan-out and more entries in each internal node of a B+-tree than in the corresponding B-tree. The leaf nodes of the B+-tree will have the same number of values and pointers, except that the pointers are data pointers and a next pointer. Hence, the order pleaf for the leaf nodes can be calculated as follows:

(pleaf * (Pr + V)) + P ≤ B (pleaf * (7 + 9)) + 6 ≤ 512 (16 * pleaf) ≤ 506

It follows that each leaf node can hold up to pleaf = 31 key value/data pointer combi-nations, assuming that the data pointers are record pointers.

As with the B-tree, we may need additional information—to implement the inser-tion and deletion algorithms—in each node. This information can include the type of node (internal or leaf), the number of current entries q in the node, and pointers to the parent and sibling nodes. Hence, before we do the above calculations for p and pleaf, we should reduce the block size by the amount of space needed for all such information. The next example illustrates how we can calculate the number of entries in a B+-tree.

Example 6. Suppose that we construct a B+-tree on the field in Example 5. To calculate the approximate number of entries in the B+-tree, we assume that each node is 69 percent full. On the average, each internal node will have 34 * 0.69 or approximately 23 pointers, and hence 22 values. Each leaf node, on the average, will hold 0.69 * pleaf = 0.69 * 31 or approximately 21 data record pointers. A B+-tree will have the following average number of entries at each level:

For the block size, pointer size, and search field size given above, a three-level B+-tree holds up to 255,507 record pointers, with the average 69 percent occupancy of nodes. Compare this to the 65,535 entries for the corresponding B-tree in Example 4. This is the main reason that B+-trees are preferred to B-trees as indexes to data-base files.

Search, Insertion, and Deletion with B+-Trees. Algorithm 18.2 outlines the procedure using the B+-tree as the access structure to search for a record. Algorithm 18.3 illustrates the procedure for inserting a record in a file with a B+-tree access structure. These algorithms assume the existence of a key search field, and they must be modified appropriately for the case of a B+-tree on a nonkey field. We illustrate insertion and deletion with an example.

Algorithm 18.2. Searching for a Record with Search Key Field Value K, Using a B+-tree

n ← block containing root node of B+-tree; read block n;

while (n is not a leaf node of the B+-tree) do begin

q ← number of tree pointers in node n;

if K ≤ n.K1 (*n.Ki refers to the ith search field value in node n*) then n ← n.P1 (*n.Pi refers to the ith tree pointer in node n*)

else if K > n.Kq−1 then n ← n.Pq else begin

search node n for an entry i such that n.Ki−1 < K ≤n.Ki;

n ← n.Pi end;

read block n end;

search block n for entry (Ki, Pri) with K = Ki; (* search leaf node *) if found

then read data file block with address Pri and retrieve record else the record with search field value K is not in the data file;

Algorithm 18.3. Inserting a Record with Search Key Field Value K in a B+-tree of Order p

n ← block containing root node of B+-tree; read block n; set stack S to empty;

while (n is not a leaf node of the B+-tree) do begin

push address of n on stack S;

(*stack S holds parent nodes that are needed in case of split*) q ← number of tree pointers in node n;

if K ≤n.K1 (*n.Ki refers to the ith search field value in node n*)

then n ← n.P1 (*n.Pi refers to the ith tree pointer in node n*) else if K > n.Kq−1

then n ← n.Pq else begin

search node n for an entry i such that n.Ki−1 < K fn.Ki;

n ← n.Pi end;

read block n

end;

search block n for entry (Ki,Pri) with K = Ki; (*search leaf node n*) if found

then record already in file; cannot insert

else (*insert entry in B+-tree to point to record*) begin

create entry (K, Pr) where Pr points to the new record; if leaf node n is not full

then insert entry (K, Pr) in correct position in leaf node n

else begin (*leaf node n is full with pleaf record pointers; is split*) copy n to temp (*temp is an oversize leaf node to hold extra

entries*);

insert entry (K, Pr) in temp in correct position;

(*temp now holds pleaf + 1 entries of the form (Ki, Pri)*)

new ← a new empty leaf node for the tree; new.Pnext ← n.Pnext ; j ← (pleaf + 1)/2 ;

n ← first j entries in temp (up to entry (Kj, Prj)); n.Pnext ← new; new ← remaining entries in temp; K ← Kj ;

(*now we must move (K, new) and insert in parent internal node; however, if parent is full, split may propagate*)

finished ← false; repeat

if stack S is empty

then (*no parent node; new root node is created for the tree*) begin

root ← a new empty internal node for the tree; root ← <n, K, new>; finished ← true;

end else begin

n ← pop stack S;

if internal node n is not full then

begin (*parent node not full; no split*)

insert (K, new) in correct position in internal node n; finished ← true

end

else begin (*internal node n is full with p tree pointers; overflow condition; node is split*)

copy n to temp (*temp is an oversize internal node*); insert (K, new) in temp in correct position;

(*temp now has p + 1 tree pointers*)

new ← a new empty internal node for the tree; j ← ((p + 1)/2 ;

n ← entries up to tree pointer Pj in temp;

(*n contains <P1, K1, P2, K2, ..., Pj−1, Kj−1, Pj >*) new ← entries from tree pointer Pj+1 in temp;

(*new contains < Pj+1, Kj+1, ..., Kp−1, Pp, Kp, Pp+1 >*)

K ← Kj

(*now we must move (K, new) and insert in parent internal node*)

end

end until finished end;

end;

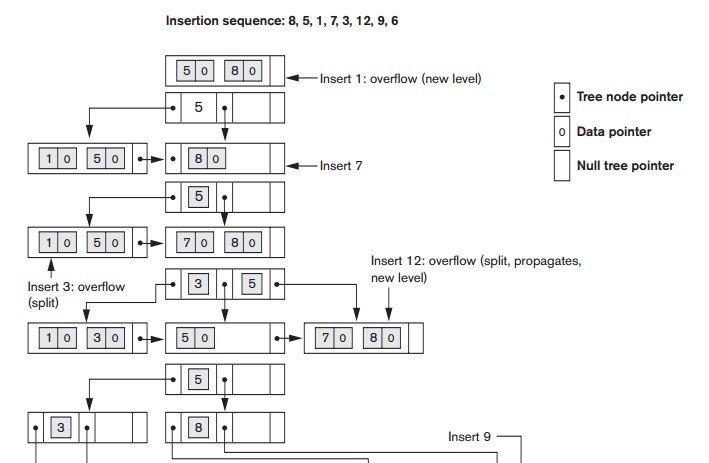
Figure 18.12 illustrates insertion of records in a B+-tree of order p = 3 and pleaf = 2. First, we observe that the root is the only node in the tree, so it is also a leaf node. As soon as more than one level is created, the tree is divided into internal nodes and leaf nodes. Notice that every key value must exist at the leaf level, because all data pointers are at the leaf level. However, only some values exist in internal nodes to guide the search. Notice also that every value appearing in an internal node also appears as the rightmost value in the leaf level of the subtree pointed at by the tree pointer to the left of the value.

When a leaf node is full and a new entry is inserted there, the node overflows and

must be split. The first j = ((pleaf + 1)/2) entries in the original node are kept there, and the remaining entries are moved to a new leaf node. The jth search value

is replicated in the parent internal node, and an extra pointer to the new node is created in the parent. These must be inserted in the parent node in their correct sequence. If the parent internal node is full, the new value will cause it to overflow also, so it must be split. The entries in the internal node up to Pj—the jth tree pointer after inserting the new value and pointer, where j = ((p + 1)/2) —are kept, while the jth search value is moved to the parent, not replicated. A new internal node will hold the entries from Pj+1 to the end of the entries in the node (see Algorithm 18.3). This splitting can propagate all the way up to create a new root node and hence a new level for the B+-tree.

Figure 18.13 illustrates deletion from a B+-tree. When an entry is deleted, it is always removed from the leaf level. If it happens to occur in an internal node, it must also be removed from there. In the latter case, the value to its left in the leaf node must replace it in the internal node because that value is now the rightmost entry in the subtree. Deletion may cause underflow by reducing the number of entries in the leaf node to below the minimum required. In this case, we try to find a sibling leaf node—a leaf node directly to the left or to the right of the node with underflow

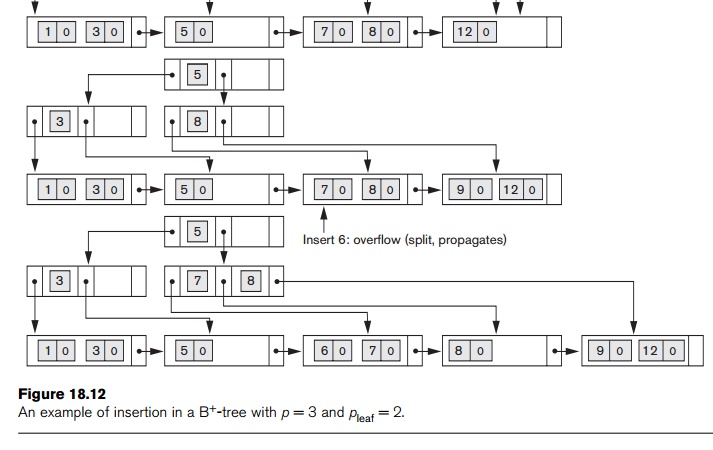
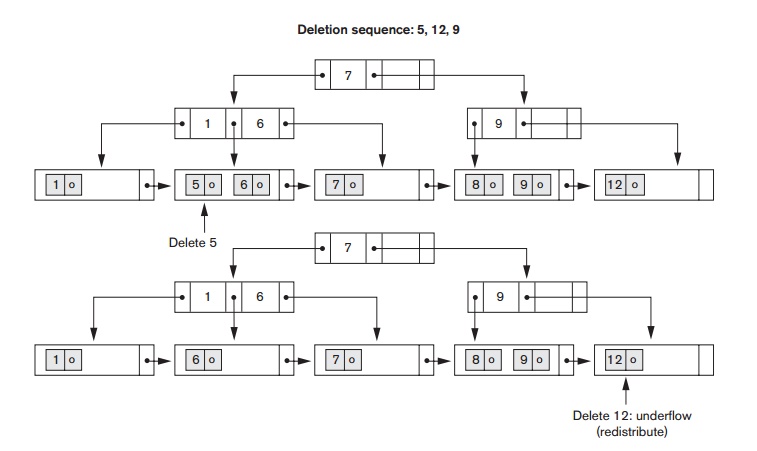
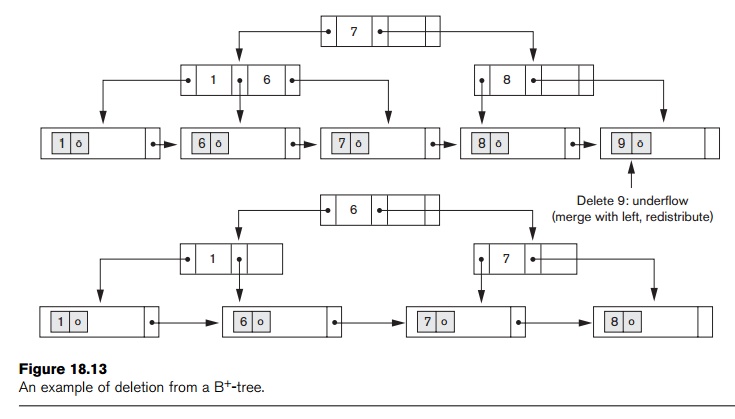
and redistribute the entries among the node and its sibling so that both are at least half full; otherwise, the node is merged with its siblings and the number of leaf nodes is reduced. A common method is to try to redistribute entries with the left sibling; if this is not possible, an attempt to redistribute with the right sibling is made. If this is also not possible, the three nodes are merged into two leaf nodes. In such a case, underflow may propagate to internal nodes because one fewer tree pointer and search value are needed. This can propagate and reduce the tree levels.

Notice that implementing the insertion and deletion algorithms may require parent and sibling pointers for each node, or the use of a stack as in Algorithm 18.3. Each node should also include the number of entries in it and its type (leaf or internal). Another alternative is to implement insertion and deletion as recursive procedures.

Variations of B-Trees and B+-Trees. To conclude this section, we briefly mention some variations of B-trees and B+-trees. In some cases, constraint 5 on the B-tree (or for the internal nodes of the B+–tree, except the root node), which requires each node to be at least half full, can be changed to require each node to be at least two-thirds full. In this case the B-tree has been called a B*-tree. In general, some systems allow the user to choose a fill factor between 0.5 and 1.0, where the latter means that the B-tree (index) nodes are to be completely full. It is also possible to specify two fill factors for a B+-tree: one for the leaf level and one for the internal nodes of the tree. When the index is first constructed, each node is filled up to approximately the fill factors specified. Some investigators have suggested relaxing the requirement that a node be half full, and instead allow a node to become completely empty before merging, to simplify the deletion algorithm. Simulation studies show that this does not waste too much additional space under randomly distributed insertions and deletions.