Chapter: Fundamentals of Database Systems : File Structures, Indexing, and Hashing : Indexing Structures for Files
Multilevel Indexes
Multilevel Indexes
The
indexing schemes we have described thus far involve an ordered index file. A
binary search is applied to the index to locate pointers to a disk block or to
a record (or records) in the file having a specific index field value. A binary
search requires approximately (log2bi) block accesses for an index with bi blocks because each step
of the algorithm reduces the part of the index file that we continue to search
by a factor of 2. This is why we take the log function to the base 2. The idea
behind a multilevel index is to
reduce the part of the index that we continue to search by bfri, the blocking factor for the index, which
is larger than 2. Hence, the search space is reduced much faster. The value bfri is called the fan-out of the multilevel index, and we
will refer to it by the symbol fo. Whereas we divide the record
search space into two halves at each step during a binary search, we divide
it n-ways (where n = the fan-out) at each search step using the multilevel index.
Searching a multilevel index requires approximately (logfobi) block accesses, which is
a substantially smaller number than for a binary search if the fan-out is
larger than 2. In most cases, the fan-out is much larger than 2.
A
multilevel index considers the index file, which we will now refer to as the first (or base) level of a
multilevel index, as an ordered file with a distinct value for each K(i). Therefore, by considering the
first-level index file as a sorted data file, we can create a primary index for
the first level; this index to the first level is called the second level of the multilevel index. Because the second level is a
primary index, we can use block
anchors so that the second level has one entry for each block of the first level. The blocking factor bfri for the second level—and
for all subsequent levels—is the same as that for the first-level index because
all index entries are the same size; each has one field value and one block
address. If the first level has r1
entries, and the blocking factor—which is also the fan-out—for the index is bfri = fo, then the first level needs (r1/fo) blocks, which is therefore the
number of entries r2
needed at the second level of the index.
We can
repeat this process for the second level. The third level, which is a primary index for the second level, has an
entry for each second-level block, so the number of third-level entries is r3 = (r2/fo) . Notice
that we require a second level only if the first level needs more than one
block of disk storage, and, similarly, we require a third level only if the
second level needs more than one block. We can repeat the preceding process
until all the entries of some index level t
fit in a single block. This block at the tth
level is called the top index level.4
Each level reduces the number of entries at the previous level by a factor of fo—the index fan-out—so we can use the
formula 1 ≤ (r1/((fo)t)) to calculate t. Hence, a multilevel index with r1 first-level entries will
have approximately t levels, where t = (logfo(r1)) . When searching the
index, a single disk block is retrieved at each level. Hence, t disk blocks are accessed for an index
search, where t is the number of index levels.
The
multilevel scheme described here can be used on any type of index—whether it is
primary, clustering, or secondary—as long as the first-level index has distinct val-ues for K(i) and fixed-length
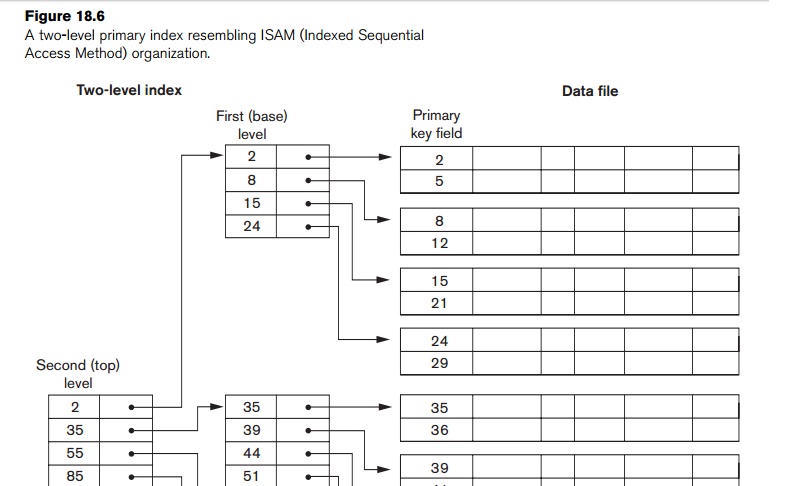
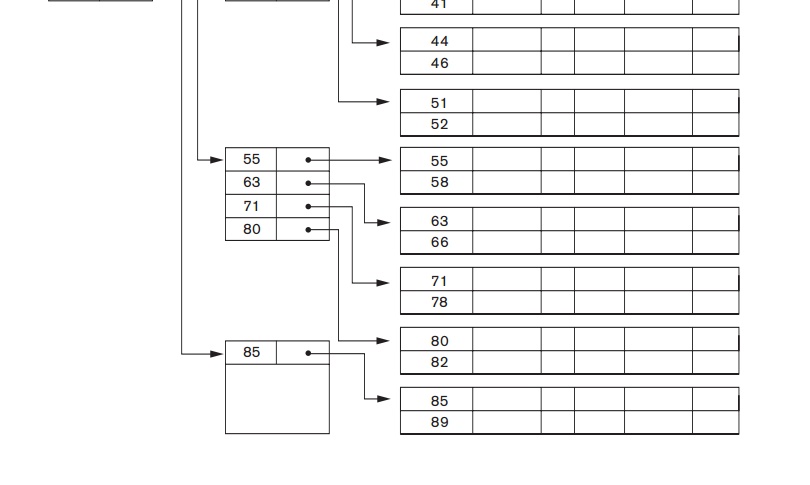
entries. Figure 18.6 shows a multilevel index built over a primary index. Example 3 illustrates
the improvement in number of blocks accessed when a multilevel index is used to
search for a record.
Example 3. Suppose that the dense secondary
index of Example 2 is converted into
a
multilevel index. We calculated the index blocking factor bfri = 68 index entries per block, which is also the
fan-out fo for the multilevel index;
the number of first-level blocks b1
= 442 blocks was also calculated. The number of second-level blocks will be b2 = (b1/fo) =
(442/68) = 7 blocks, and the number of third-level blocks will be b3 = (b2/fo) =
(7/68) = 1 block. Hence, the third level is the top level of the index, and t = 3. To access a record by searching
the multilevel index, we must access one block at each level plus one block
from the data file, so we need t + 1
= 3 + 1 = 4 block accesses. Compare this to Example 2, where 10 block accesses
were needed when a single-level index and binary search were used.
Notice
that we could also have a multilevel primary index, which would be non-dense.
Exercise 18.18(c) illustrates this case, where we must access the data block from the file before we can determine
whether the record being searched for is in the file. For a dense index, this
can be determined by accessing the first index level (without having to access
a data block), since there is an index entry for every record in the file.
A common
file organization used in business data processing is an ordered file with a
multilevel primary index on its ordering key field. Such an organization is
called an indexed sequential file
and was used in a large number of early IBM systems. IBM’s ISAM organization incorporates a two-level index that is closely
related to the organization of the disk in terms of cylinders and tracks (see
Section 17.2.1). The first level is a cylinder index, which has the key value
of an anchor record for each cylinder of a disk pack occupied by the file and a
pointer to the track index for the cylinder. The track index has the key value
of an anchor record for each track in the cylinder and a pointer to the track.
The track can then be searched sequentially for the desired record or block.
Insertion is handled by some form of overflow file that is merged periodically
with the data file. The index is recreated during file reorganization.
Algorithm
18.1 outlines the search procedure for a record in a data file that uses a
nondense multilevel primary index with t
levels. We refer to entry i at level j of the index as <Kj(i), Pj(i)>, and we search for a record whose
primary key value is K. We assume
that any overflow records are ignored. If the record is in the file, there must
be some entry at level 1 with K1(i) f K < K1(i + 1) and
the record will be in the block of the data file whose address is P1(i). Exercise 18.23 discusses modifying the search algorithm for
other types of indexes.
Algorithm 18.1. Searching a Nondense Multilevel
Primary Index with t
Levels
(* We assume the index entry to be a block
anchor that is the first key per block. *) p ← address of top-level block of
index;
for j ← t step – 1 to 1 do begin
read the
index block (at jth index level)
whose address is p; search block p for entry i such that Kj
(i) ≤ K < Kj(i + 1)
(* if Kj(i)
is the
last entry in the block, it is sufficient to satisfy Kj(i) ≤ K *); p ← Pj(i ) (* picks appropriate pointer at jth index level *)
end;
read the
data file block whose address is p;
search block p for record with key = K;
As we
have seen, a multilevel index reduces the number of blocks accessed when
searching for a record, given its indexing field value. We are still faced with
the problems of dealing with index insertions and deletions, because all index
levels are physically ordered files. To
retain the benefits of using multilevel indexing while reducing index insertion and deletion problems, designers adopted
a multilevel index called a dynamic
multilevel index that leaves some space in each of its blocks for inserting
new entries and uses appropriate insertion/deletion algorithms for creating
and deleting new index blocks when the data file grows and shrinks. It is often
implemented by using data structures called B-trees and B+-trees, which
we describe in the next section.
Related Topics