Real Number System

Real Number System

First we shall recall how the real number system was developed. We start with natural numbers N.

1. Rational Numbers

Note that N = {1, 2, 3, . . . } is enough for counting objects. In order to deal with loss or debts, we enlarged N to the set of all integers, Z = {. . . , −4, −3, −2, −1, 0, 1, 2, . . .} , which consists of the natural numbers, zero, and the negatives of natural numbers. We call {0, 1, 2, 3, · · · } as the set of whole numbers and denote it by W. Note that it differs from N by just one element, namely, zero. Now imagine dividing a cake into five equal parts, which is equivalent to finding a solution of 5x = 1. But this equation cannot be solved within Z. Hence we have enlarged Z to the set Q –{ m/n | m, nÎZ, n¹0}  of ratios; so we call each x ∈ Q as a rational number. Some examples of rational numbers are

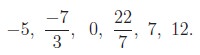
We have seen in earlier classes that rational numbers are precisely the set of terminating or infinite periodic decimals. For example,

2. The Number Line

Let us recall “The Number Line”. It is a horizontal line with the origin, to represent 0, and another point marked to the right of 0 to represent 1. The distance from 0 to 1 defines one unit of length. Now put 2 one unit to the right of 1. Similarly we put any positive rational number x to the right of 0 and x units away. Also, we put a negative rational number −r, r > 0, to the left of 0 by r units. Note that for any x, y ∈ Q if x<y, then x is to the left of y; also x < (x + y)/2  < y and hence between any two distinct rational numbers there is another rational number between them.

Question:

Have we filled the whole line with rational numbers?

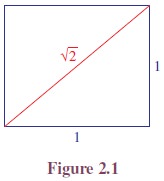
The answer to the above question is “No” as the following consideration demonstrates. Consider a square whose side has length 1 unit. Then by Pythagoras theorem its diagonal has length √2 units.

3. Irrational Numbers

Theorem 2.1: √2 is not a rational number.

Proof. Suppose that √2 is a rational number. Let √2 = m /n , where m and n are positive integers with no common factors greater than 1. Then, we have m² = 2n², which implies that m² is even and hence m is even.

Let m = 2k. Then, we have 2n² = 4k² which gives n² = 2k².

Thus, n is also even.

It follows, that m and n are even numbers having a common factor 2.

Thus, we arrived at a contradiction.

Hence, √2 is an irrational number.

Remark:

(i) Note that in the above proof we have assumed the contrary of what we wanted to prove and arrived at a contradiction. This method of proof is called ‘proof by contradiction’.

(ii) There are points on the number line that are not represented by rational numbers.

(iii) We call those numbers on the number line that do not correspond to rational numbers as irrational numbers. The set of all irrational numbers is denoted by Q’ (For number line see Figure 1.2.)

Every real number is either a rational number or an irrational number, but not both. Thus, R = Q ∪ Q’ and Q ∩ Q’ = ∅.

As we already knew that every terminating or infinite periodic decimal is a rational number, we see that the decimal representation of an irrational number will neither be terminating nor infinite periodic. The set R of real numbers can be visualized as the set of points on the number line such that if x < y, then x lies to left of y.

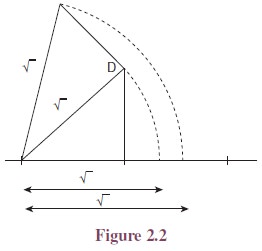
Figure 2.2 demonstrates how the square roots of 2 and 3 can be identified on a number line.

We notice that N ⊂ W ⊂ Z ⊂ Q ⊂ R.

As we have already observed, irrational numbers occur in real life situations. Over 2000 years ago people in the Orient and Egypt observed that the ratio of the circumference to the diameter is the same for any circle. This constant was proved to be an irrational number by Johann Heinrich Lambert in 1767. The value of π rounded off to nine decimal places is equal to 3.141592654. The values 22/7 and 3.14, used in calculations, such as area of a circle or volume of a sphere, are only approximate values for π.

The number π, which is the ratio of the circumference of a circle to its diameter, is an irrational number.

Now let us recall the properties of the real number system which is the foundation for mathematics.

4. Properties of Real Numbers

(i) For any a, b ∈ R, a + b ∈ R and ab ∈ R.

[Sum of two real numbers is again a real number and multiplication of two real numbers is again a real number.]

(ii) For any a, b, c ∈ R, (a + b) + c = a + (b + c) and a(bc)=(ab)c.

[While adding (or multiplying) finite number of real numbers, we can add (or multiply) by grouping them in any order.]

(iii) For all a ∈ R, a +0= a and a(1) = a.

(iv) For every a ∈ R, a + (−a)=0 and for every b ∈ R − {0}, b (1/b) = 1.

(v) For any a, b ∈ R, a + b = b + a and ab = ba.

(vi) For a, b, c ∈ R, a(b + c) = ab + ac.

(vii) For a, b ∈ R,a<b if and only if b − a > 0.

(viii) For any a ∈ R, a² ≥ 0.

(ix) For any a, b ∈ R, only one of the following holds: a = b or a<b or a > b.

(x) If a, b ∈ R and a < b, then a + c<b + c for all c ∈ R.

(xi) If a, b ∈ R and a < b, then ax < bx for all x > 0.

(xii) If a, b ∈ R and a < b, then ay > by for all y < 0.