Rational Functions

Rational Functions

A rational expression of x is defined as the ratio of two polynomials in x, say P (x) and Q(x) where

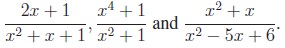
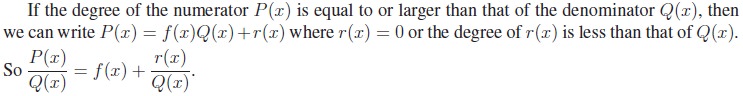
1. Rational Inequalities

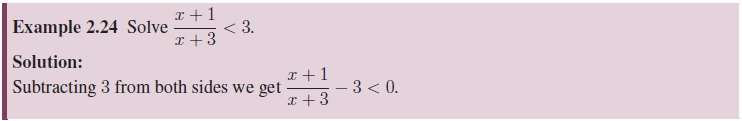
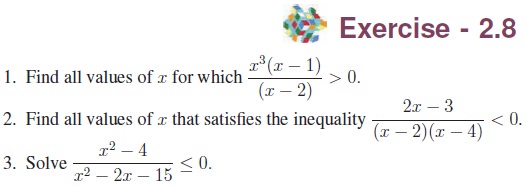
2. Partial Fractions

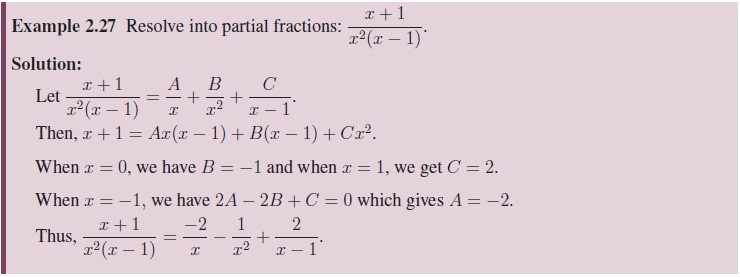
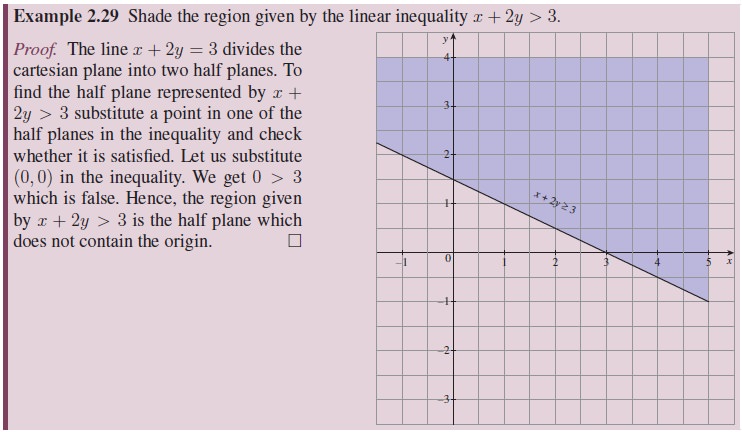
3. Graphical Representation of Linear Inequalities

A straight line ax + by = c divides the Cartesian plane into two parts. Each part is an half plane. A vertical line x = c will divide the plane in left and right half planes and a horizontal line y = k will divide the plane into upper and lower half planes.

A point in the cartesian plane which is not on the line ax + by = c will lie in exactly one of the two half planes determined by the line and satisfies one of the inequalities ax + by < c or ax + by > c.

To identify the half plane represented by ax + by < c, choose a point P in any one of the half planes and substitute the coordinates of P in the inequality.

If the inequality is satisfied, then the required half plane is the one that contains P; otherwise the required half plane is the one that does not contain P. When c ¹ 0, it is most convenient to take P to be the origin.

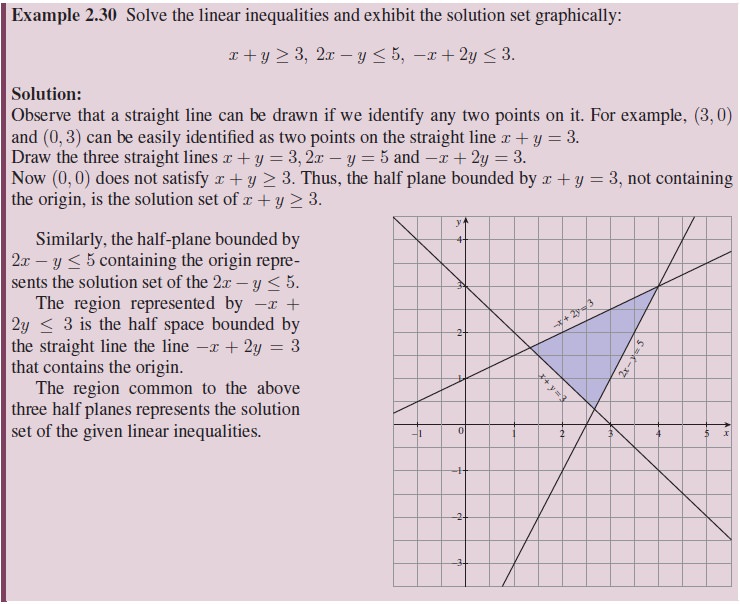
                                                   Exercise - 2.10

Determine the region in the plane determined by the inequalities:

(1) x ≤ 3y, x ≥ y.

(2) y ≥ 2x, −2x + 3y ≤ 6.

(3) 3x + 5y ≥ 45, x ≥ 0, y ≥ 0.

(4) 2x + 3y ≤ 35, y ≥ 2, x ≥ 5.

(5) 2x + 3y ≤ 6, x + 4y ≤ 4, x ≥ 0, y ≥ 0.

(6) x − 2y ≥ 0, 2x − y ≤ −2, x ≥ 0, y ≥ 0.

(7) 2x + y ≥ 8, x + 2y ≥ 8, x + y ≤ 6.