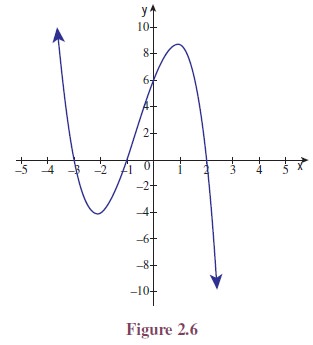
Polynomial Functions

Polynomial Functions

1. Division Algorithm

Given two polynomials f(x) and g(x), where g(x) is not the zero polynomial, there exist two polynomials q(x) and r(x) such that f(x) = q(x)g(x) + r(x) where degree of r(x) < degree of g(x). Here, q(x) is called the quotient polynomial, and r(x) is called the remainder polynomial. If r(x) is the zero polynomial, then q(x), g(x) are factors of f(x) and f(x) = q(x)g(x).

These terminologies are similar to terminologies used in division done with integers.

If g(x) = x − a, then the remainder r(x) should have degree zero and hence r(x) is a constant. To determine the constant, write f(x) = (x − a)q(x) + c. Substituting x = a we get c = f(a).

Remainder Theorem

If a polynomial f(x) is divided by x−a, then the remainder is f(a). Thus the remainder c = f(a) = 0 if and only if x − a is a factor for f(x).

In general, if we can express f(x) as f(x) = (x − a)^k.g(x) where g(a) = 0, then the value of k, which depends on a, cannot exceed the degree of f(x). The value k is called the multiplicity of the zero a.

Two important problems relating to polynomials are

i.            Finding zeros of a given polynomial function; and hence factoring the polynomial into linear factors and

ii.            Constructing polynomials with the given zeros and/or satisfying some additional conditions.

To address the problem of finding zeros of a polynomial function, some well known algebraic identities are useful. What is an identity?

An equation is said to be an identity if that equation remains valid for all values in its domain. An equation is called conditional equation if it is true only for some (not all) of values in its domain. Let us recall the following identities.

2. Important Identities

Method of Undetermined Coefficients

Now let us focus on constructing polynomials with the given information using the method of undetermined coefficients. That is, we shall determine coefficients of the required polynomial using the given conditions. The main idea here is that two polynomials are equal if and only if the coefficients of same powers of the variables in the two polynomials are equal.