Quadratic Functions

Quadratic Functions

In earlier classes we have learnt that for any z ∈ R and n ∈ N, zⁿ = z · z · z · · · z (n-times).

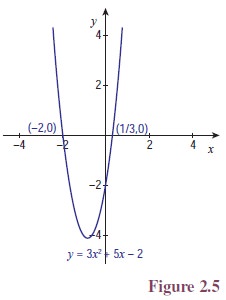
A function of the form P (x) = ax² + bx + c, where a, b, c ∈ R are constants and a ¹ 0, is called a quadratic function. If P (t) = 0 for some t ∈ R, then we say t is a zero of P (x).

1. Quadratic Formula

2. Quadratic Inequalities

Here we shall learn to solve the quadratic inequalities ax² + bx + c < 0 or ax² + bx + c > 0.

Steps to Solve Quadratic Inequalities:

i.            First solve ax² + bx + c = 0.

ii.            If there are no real solutions, then one of the above inequality holds for all x ∈ R

iii.            If there are real solutions, which are called critical points, then label those points on the number line.

iv.            Note that these critical points divide the number line into disjoint intervals. (It is possible that there may be only one critical point.)

v.            Choose one representative number from each interval.

vi.            Substitute that these representative numbers in the inequality.

vii.            Identify the intervals where the inequality is satisfied.