Definition, Properties, Equations Formula, Solved Example Problems, Exercise | Algebra | Mathematics - Absolute Value | 11th Mathematics : UNIT 2 : Basic Algebra
Chapter: 11th Mathematics : UNIT 2 : Basic Algebra
Absolute Value
Absolute Value
1. Definition and Properties
As we have observed
that there is an order preserving one-to-one correspondence between elements of
R and points on the number line. Note that for
each x ∈ R, x and −x are equal distance
from the origin. The distance of the number a ∈ R from 0 on the number line is called the absolute value of that number a and is denoted by |a|. Thus, for any x ∈ R, we have
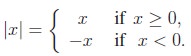
and hence |·| defines a function
known as absolute value function, from R onto [0, ∞).
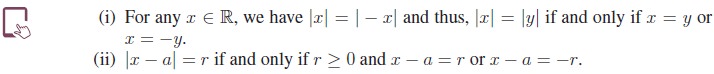
2. Equations Involving Absolute Value
Note that a real number a is said to be a solution of an equation or an inequality, if the statement obtained after replacing the variable by a is true.
Next we shall learn
solving equations involving absolute value.

3. Some Results For Absolute Value
(i) If x, y ∈ R, |y + x| = |x − y|, then xy = 0.
(ii) For any x, y ∈ R, |xy| = |x||y|.
(iii) |x/y| = |x/y|,
for all x, y ∈ R and y ¹ 0.
(iv) For any x, y ∈ R, |x + y|≤|x| + |y|.
4. Inequalities Involving Absolute Value
Here we shall learn to
solve inequalities involving absolute values. First we analyze very simple
inequalities such as (i) |x| < r and (ii) |x| > r.
(i) Let us prove that
|x| < r if and only if −r<x<r. Note that r > 0 as |x| ≥ 0.
There are two
possibilities to consider depending on the sign of x.
Case (1). If x ≥ 0,
then |x| = x, so |x| < r implies x<r.
Case (2). If x < 0,
then |x| = −x, so |x| < r implies −x<r that is, x > −r.
Therefore we have, |x|
< r if and only if −r < x < r, that is x ∈ (−r, r).
(ii) Let us prove that
|x| > r if and only if x < −r or x>r.
Consider |x| > r.
If r < 0, then every x ∈ R satisfies the
inequality.
For r ≥ 0, there are
two possibilities to consider.
Case (1). If x ≥ 0, then
|x| = x>r.
Case (2). If x < 0,
then |x| = −x>r, that is, x < −r.
So we have |x| > r,
if and only if x < −r or x > r, that is, x ∈ (−∞, −r) ∪ (r, ∞).
Remark:
(i) For any a ∈ R, |x − a| ≤ r if and only if −r ≤ x − a ≤ r if and only if x ∈ [a − r, a + r].
(ii) For any a ∈ R, |x − a| ≥ r is equivalent to x − a ≤ −r or x − a ≥ r if and
only if x ∈ (−∞, a − r] ∪ [a + r, ∞).

Related Topics