Definition, Properties, Proof, Solved Example Problems, Exercise | Mathematics - Logarithm | 11th Mathematics : UNIT 2 : Basic Algebra
Chapter: 11th Mathematics : UNIT 2 : Basic Algebra
Logarithm
Logarithm
We have seen that,
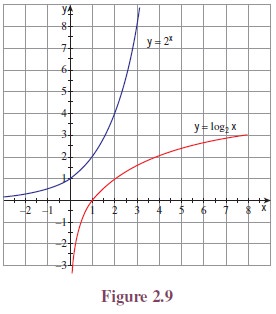
with a base 0 < a ¹ 1, the exponential function f(x) = ax is defined on R having range (0, ∞). We also observed that f(x) is a bijection, hence it has an inverse. We
call this inverse function as logarithmic function and is denoted by loga(.). Let us discuss this
function further. Note that if f(x)
takes x to y = ax, then loga(.) takes y to x. That is, for 0 < a ¹
1, we have
y
= ax is equivalent to loga y = x.
For example, since 34 = 81 we have log3(81) = 4. In other words, with
fixed a, given a real number y, logarithm finds the
exponent x satisfying ax = y. This is useful in
addressing practical problems like, “how long will it take for certain
investment to reach a fixed amount?” Logarithm is also very useful in
multiplying very small or big numbers.

Properties of Logarithm






Related Topics