Definition, Formula, Solved Example Problems, Exercise | Mathematics - Exponents and Radicals | 11th Mathematics : UNIT 2 : Basic Algebra
Chapter: 11th Mathematics : UNIT 2 : Basic Algebra
Exponents and Radicals
Exponents and Radicals
First we shall consider exponents.
1. Exponents
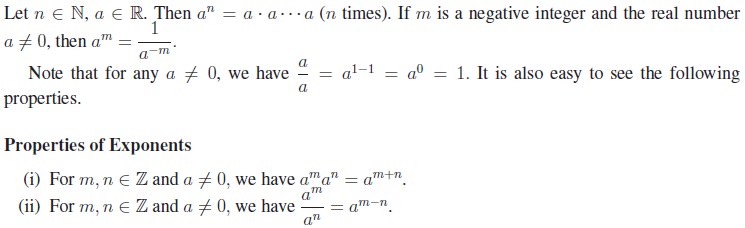
2. Radicals
Question:


3. Exponential Function

Properties of
Exponential Function
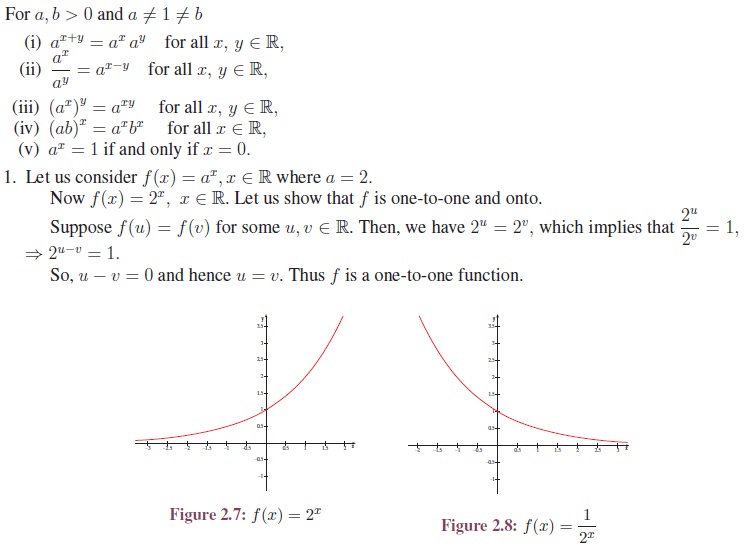

A Special
Exponential Function
Among all exponential
functions, f(x) = ex, x ∈ R is the most important one as it has
applications in many areas like mathematics, science and economics. Then what
is this e? The following illustration from compounding interest problem
leads to the constant e.
Illustration
Compound
Interest


We notice that as n gets really large, An values seem to be
getting closer to 2.718281815..... Actually An values approach a real
number e, an irrational number. 2.718281815 is an approximation to e. So the compound interest
formula becomes A = P ert, where r is the interest rate and P is the principal and t is the number of years. This is called Continuous Compounding.



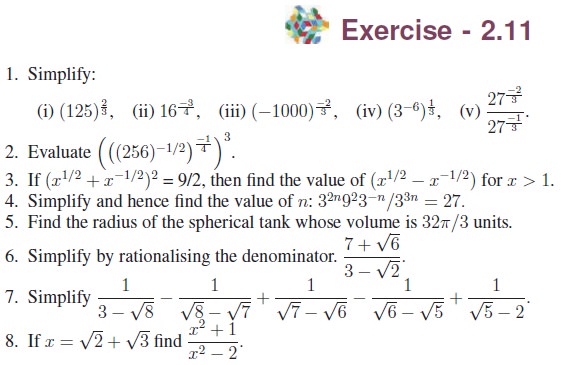
Related Topics