Proton nuclear magnetic resonance spectroscopy

PROTON NUCLEAR MAGNETIC RESONANCE SPECTROSCOPY

Key Notes

Secondary magnetic fields

The presence of secondary magnetic fields in a molecule means that non-equivalent protons experience slightly different magnetic fields when the external magnetic field is applied. This means that different protons require different energies for resonance and give different signals in a spectrum.

Secondary magnetic fields due to electrons

Electrons are charged spinning bodies, which set up a secondary magnetic field that opposes the applied field and shields the proton. The greater the electron density around a proton, the greater the shielding and the less energy is required for resonance.

The nmr spectrum

The protons which give signals at the right hand side of an nmr spectrum are more shielded than those at the left-hand side and require less energy to resonate. The scale used in nmr is known as the chemical shift which is measured in parts per million relative to the signal for a reference compound called tetramethylsilane.

Inductive effects on chemical shift

The position of a signal in the nmr spectrum is affected by the inductive effects of various groups. Electron donating groups increase the electron density round a neighboring proton and lower the chemical shift. Electron withdrawing groups have the opposite effect.

Diamagnetic circulation

If an unsaturated group is present in a molecule, it is possible to get secondary magnetic fields due to diamagnetic circulation. This is a result of the external magnetic field causing the π electrons to circulate around the axis of the magnetic field. The effect is large for aromatic rings since six π electrons are involved, and smaller for groups such as alkenes and ketones. For most unsaturated systems, the secondary magnetic field enhances the applied magnetic field and increases chemical shift. The protons of aldehy-des and carboxylic acids experience secondary magnetic fields due to dia-magnetic circulation as well as electron withdrawing inductive effects, resulting in very large chemical shifts.

Integration

Integration measures the relative intensity of each signal in the nmr spectrum and is proportional to the number of protons responsible for that signal.

Secondary magnetic fields

At this stage, we can see how a proton is detected by nmr spectroscopy, but if that was  all  there  was  to  it  we  would  only  see  one  signal  for  every  proton  in  a molecule. This would tell us nothing about the structure apart from the fact that protons  are  present.  Fortunately,  not  all  protons  require  the  same  energy  for resonance.  This  is  because  there  are  secondary  magnetic  fields  within  the molecule,  which  influence  the  magnetic  field  experienced  by  each  proton. Secondary magnetic fields are produced by the electrons in the molecule and are much smaller in magnitude than the applied magnetic field – in the order of 0–10 parts per million (ppm). However, they are sufficiently large enough to result in different signals for different protons. This means that there should be one signalfor every different (or non-equivalent) proton in the structure. Therefore, it is useful to identify the number of non-equivalent protons in a molecule in order to identify the number of signals that should be present in the spectrum. Note that the protons in a methyl group are equivalent and do not give separate signals because they are in identical molecular environments. This is also true for the protons in a CH₂ group. (However, there are two situations where the two protons on a CH₂  group become non equivalent, i.e. when they are constrained within a ring  system  and  when  they  are  next  to  an  asymmetric  center.)  The  size  and direction of secondary magnetic fields depends on electron density, diamagnetic circulation and spin-spin coupling all of which are discussed below.

Secondary magnetic fields due to electrons

Fig. 3a shows an isolated proton spinning and precessing in an applied magnetic field. So far we have only considered the nucleus of the hydrogen atom, but we know that electrons must be present. Let us consider the effect of one electron orbiting the nucleus (Fig. 4).

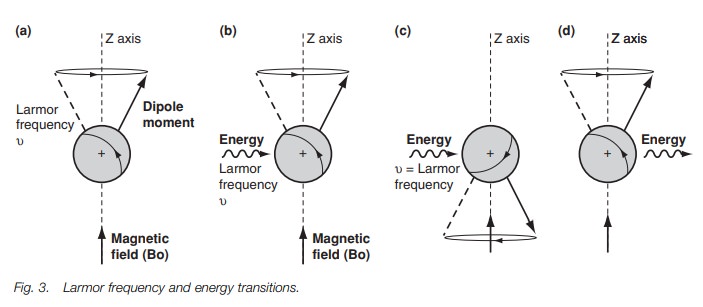
Since the electron is a spinning, charged body, it sets up a secondary magnetic Vfield of its own (Be, Fig. 4). The secondary magnetic field (Be) opposes the exter- nal magnetic field (Bo). Thus the nucleus is shielded from the external magnetic field. This means the actual magnetic field experienced by the nucleus is reduced (Bo–Be). Since the nucleus experiences a reduced magnetic field, the precessional or Larmor frequency is reduced. This in turn means that less energy is required to make that nucleus resonate and give a signal. The greater the electron density round a proton, the greater the shielding and so the position of a signal in an nmrspectrum can be an indication of electron density in different parts of a molecule.

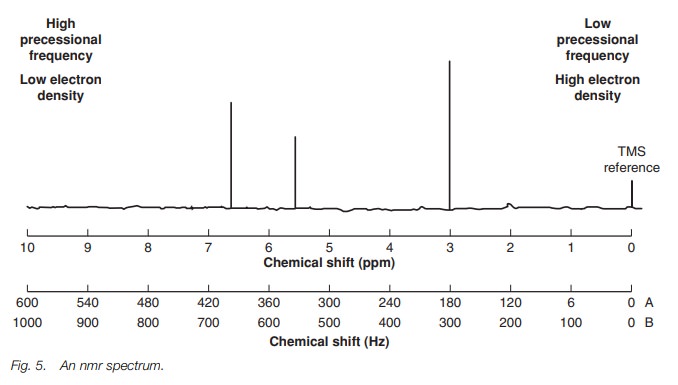
The nmr spectrum

The signals at the right hand side of an nmr spectrum (Fig. 5) are due to protons having a low precessional frequency while the signals at the left-hand side are dueto protons having a high precessional frequency. Low precessional frequency isassociated  with  high  electron  density  (shielding)  while  high  precessional frequency  is  associated  with  low  electron  density  (deshielding).  The  energyrequired for resonance increases from right to left.

A scale is needed in order to quantify the position of signals in an nmr spec-trum. The scale used in nmr does not have absolute values, but is relative to the signal of a reference compound called tetramethylsilane (TMS) (Fig. 6). The methyl protons of TMS are equivalent and give one signal that is defined as the zero point on the scale. The scale is known as the chemical shift and is measured in parts per million (ppm). What does this mean and why do we not use an absolute scale, which uses frequency or energy units?

Let us look at what happens if we measure the chemical shift in frequency units of hertz. The scale shown in Fig. 5A is for a 60 MHz nmr spectrometer. The 60 MHz refers to the frequency of the energy required to cause resonance. Thus, the signal at 3 ppm has a Larmor frequency which is 180 Hz faster than the signal due to TMS (180 Hz is 3 ppm of 60 MHz).

However, we could also measure this spectrum using a more powerful nmr spectrometer which results in the protons having precessional frequencies in the order of 100 MHz (Fig. 5b). 

In this situation, the signal at 3 ppm is due to a proton that is precessing 300 Hz faster than the protons for TMS. If we measure the chem-ical shift of this peak in ppm, this would still be 3 ppm, since 300 Hz is 3 ppm of 100 MHz. However, if we used a scale measured in Hertz, we would have to define the power of the nmr spectrometer used. With chemical shift measured in parts per million, the chemical shift will be the same no matter which instrument is used.

Inductive effects on chemicalshift

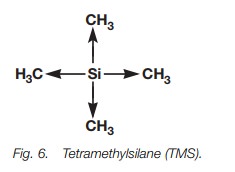
TMS is called an internal reference since it is dissolved in the deuterated solvent used to dissolve the sample. There is a good reason why TMS is used as an internal reference. Silicon has a tendency to ‘repel’ the electrons in the silicon-carbon bonds such that they are pushed towards the methyl groups (Fig. 6) – an inductive effect. This means that the protons in these methyl groups experience ahigh electron density that shields the nuclei and results in a low chemical shift, lower in fact than the vast majority of nmr signals observed in organic molecules.

Inductive effects have an important influence on chemical shift. We can see this with a series of methyl groups (Fig. 7). Going from right to left we have TMS which sets the scale at 0 ppm. Next we have the methyl group of a saturated hydrocarbon. The alkyl groups of a hydrocarbon also ‘push electrons’ away from them and hence increase electron density round a neighboring methyl group. However this inductive effect is not as powerful as the one caused by a silicon atom and so the methyl signals in hydrocarbons usually occur about 0.9 ppm.

In the next case we have a methyl group next to a ketone group. A ketone group has an electron withdrawing effect, which reduces the electron density around the neighboring methyl group (deshielding), and so the chemical shift is higher at about 2.2 ppm. The electron withdrawing effect of an oxygen atom or a positively charged nitrogen is greater still and so a methyl ether group has a signal at about 3.3 ppm, similar to the methyl signal of a quaternary ammonium salt.

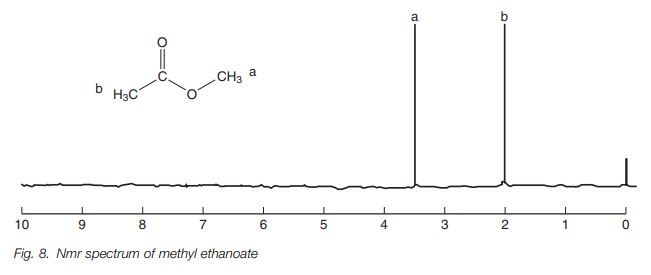
Since the position of a signal in the nmr spectrum is related to inductive effects, it is possible to use this knowledge to assign different signals in an nmr spectrum. For example, the nmr spectrum for methyl ethanoate contains two signals at 2.0 and 3.5 ppm (Fig. 8). The signal at 3.5 ppm can be assigned to CH₃^a since it is directly attached to oxygen. The oxygen has a stronger electron withdrawing effect than the carbonyl group. NMR tables are also available which show the typical chemical shifts for particular groups.

Diamagnetic circulation

A special type of secondary magnetic effect is called diamagnetic circulation. This occurs in functional groups which contain π bonds. As an example, we shall consider the aromatic ring (Fig. 9).

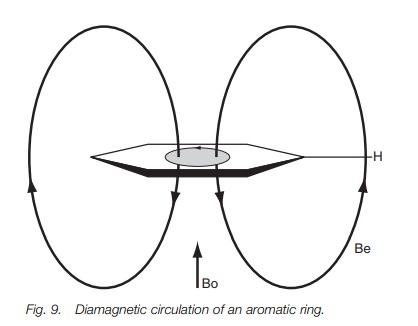
The applied external magnetic field (Bo) used in nmr has an interesting effect on the π-electrons of the aromatic ring, causing them to circulate round the ring in a process known as diamagnetic circulation. This movement in turn sets up a sec-ondary magnetic field (Be) represented by the force lines shown in Fig. 9. The direction of these lines opposes the applied magnetic field at the center of the aro-matic ring, but enhances it at the edges where the aromatic protons are situated. This means that the field observed by the aromatic protons is increased (Bo+Be) causing their precessional frequency to increase. This means that a greater energy is required for resonance, resulting in a higher chemical shift

The effect of diamagnetic circulation on aromatic protons is greater than inductive effects and this can be seen in the nmr spectrum of benzyl methyl ether (Fig. 10).

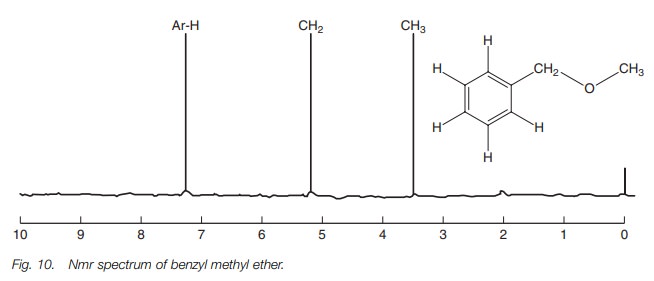
The methyl group at 3.6 ppm has a relatively high chemical shift due to the inductive effect of oxygen. The methylene group at 5.2 ppm has an even higher chemical shift since it is next to oxygen and the aromatic ring, both of which are electron withdrawing groups. However, the aromatic protons have the highest chemical shift at 7.3 ppm since they experience the secondary magnetic field set up by diamagnetic circulation.

Diamagnetic circulation is also possible for other unsaturated systems such as alkenes. However, the diamagnetic circulation for an alkene is much smaller since only two π  electrons are circulating within a double bond, and so the effect is smaller. This can be seen in the nmr spectrum of 1,1-diphenylethene where the alkene protons have a smaller chemical shift at 5.2 ppm compared to the aromatic protons at 7.3 ppm (Fig. 11).        

An aldehyde proton also experiences a secondary magnetic field due to dia- magnetic circulation, but in addition there is an inductive effect resulting from the electron withdrawing effect of the carbonyl group. Thus, an aldehyde proton experiences two deshielding effects, which means that it has a higher chemical shift than even an aromatic ring. Typically, the signal appears about 9.6 ppm.

The combined influences of diamagnetic circulation and inductive effects also result in high chemical shifts for the OH of a carboxylic acid where the signal can have a chemical shift larger than 10 ppm.   

For most unsaturated systems, diamagnetic circulation sets up a secondary field which enhances the applied magnetic field. The exception is alkynes where the secondary field opposes the applied field and causes shielding.

Integration

An nmr spectrum contains another piece of useful information which is called integration. Integration measures the intensity of each signal and is proportionalto the number of protons responsible for that signal. Thus, a signal due to a methyl group will be three times more intense than one due to a methine (CH) group.

The integration signal on the nmr spectrum is the sloping line above the signals (Fig. 19). There is no absolute scale to this line, but the relative heights of the inte-gration over each signal are proportional to the number of protons responsible for each signal. Note that it is the height increase over the whole signal that should be measured (i.e. you measure the height increase over all the peaks in the coupling pattern).

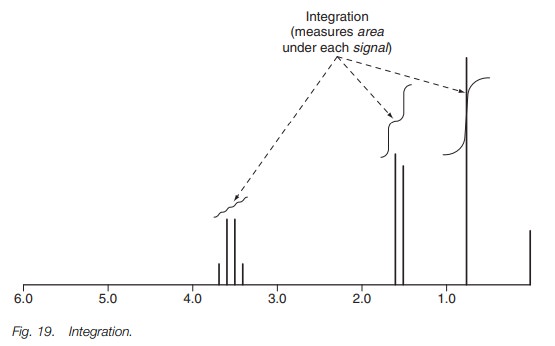
Another thing to watch out for is the possibility of OH or NH₂ groups being present in a spectrum. These will also be integrated, but can be distinguished from CH, CH₂ and CH₃ groups since the protons in the former disappear from the spectrum if the sample is shaken with D₂O.