Proton nuclear magnetic resonance spectroscopy: Introduction

PROTON NUCLEAR MAGNETIC RESONANCE SPECTROSCOPY

Key Notes

Introduction

Nmr spectroscopy involves the detection of nuclei. Nuclei are charged spin-ning bodies that have an associated magnetic moment. In proton nmr, an external magnetic field is applied to force protons into two possible orien-tations which are not of equal energy. Those nuclei spinning with their mag-netic moments aligned with the field are more stable than those spinning with their magnetic moments aligned against the field. There is a greater population of nuclei in the more stable orientation. Applying energy in the form of electromagnetic radiation causes the nuclei to flip or resonate between the two orientations resulting in an overall absorption of energy. When the radiation is stopped, the nuclei relax to the more stable popula-tion ratio resulting in an emission of energy. A spectrum can be obtained by measuring the energy absorbed or the energy emitted. The energy required for resonance is in the radiofrequency region of the electromagnetic spectrum and is equal to the frequency with which the magnetic moment precesses round the axis of the applied magnetic field. The precessional frequency increases if the applied magnetic field is increased. Nmr spectrometers and spectra are defined by the energy required for resonance.

Introduction

Of all the spectroscopic methods, nuclear magnetic resonance (nmr) spectroscopy is the most useful in determining the structure and stereochemistry of organic compounds. Nmr spectroscopy detects the nuclei of atoms in a molecule, and one of the most useful forms of nmr is the detection of hydrogen atoms. The nucleu of a hydrogen atom is a single proton and so the method is also known as protonnmr. 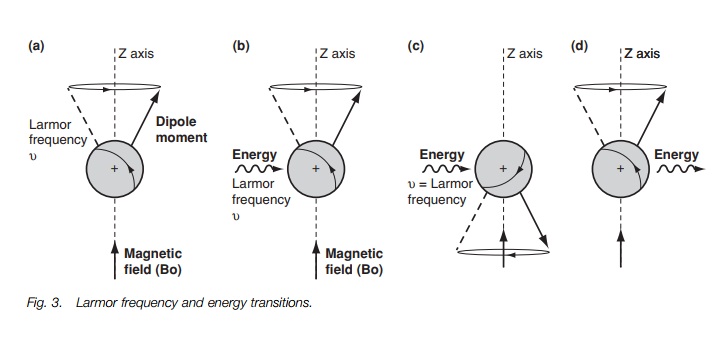A proton spins around its axis, and whenever a charged body spins, a magnetic field is set up which can be represented by a magnetic dipole moment (Fig. 1a). 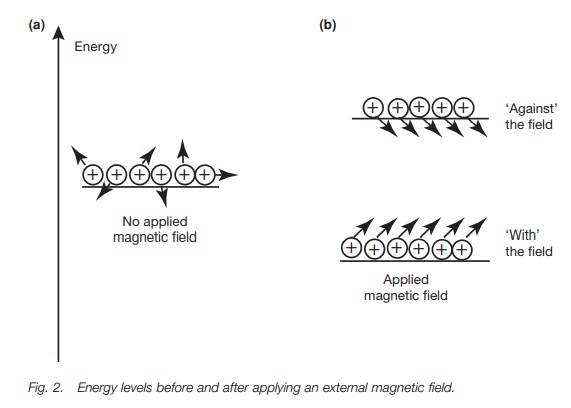Under normal conditions, the protons and their magnetic moments are randomly orientated and so there is no overall magnetic field (Fig. 2a).

However, the situation changes if an external magnetic field is applied to the sample. In Fig. 1b and c an external magnetic field has been applied in the direc- tion of the z-axis. This field interacts with the magnetic moment of the nucleus, forcing the nucleus to spin in only two possible orientations. In Fig. 1b, the nucleus is  spinning  such  that  the  magnetic  moment  is  pointing  in  roughly  the  same direction as the field. 

The other orientation (Fig. 1c) has the nucleus spinning such the dipole moment is pointed roughly against the field. Crucially, these two ori-entations are not of equal energy. The orientation against the field is less stable than the orientation with the field (Fig. 2b). This is crucial to understanding why we get an nmr spectrum.

The energy difference between the two orientations is extremely small and so the energy levels involved are almost equally populated. However, there is a slight excess of nuclei in the more stable energy level, and so if we were to pro-mote these nuclei to the higher energy level, energy would be absorbed and a spectrum could be measured. Before we look at what energy is required, we shall return to our picture of the spinning nucleus. Fig. 1b shows the nucleus spinning with the field – the more stable orientation. Notice that the dipole moment is not directly aligned with the magnetic field, but is at an angle to it. This means that the dipole moment experiences a force or a torque, which causes it to rotate or pre-cess around the z-axis (Fig. 3a) like a gyroscope. A gyroscope is a spinning body which, when set at an angle to the vertical axis of gravity, precesses round that vertical axis. The nucleus is undergoing exactly the same kind of motion. It too is a spinning body but it precesses round the axis of an applied magnetic field. The rate at which the dipole moment precesses round the z-axis is called the Larmorfrequency and is dependant on the strength of the applied magnetic field. If themagnetic field increases, the rate of precession increases.

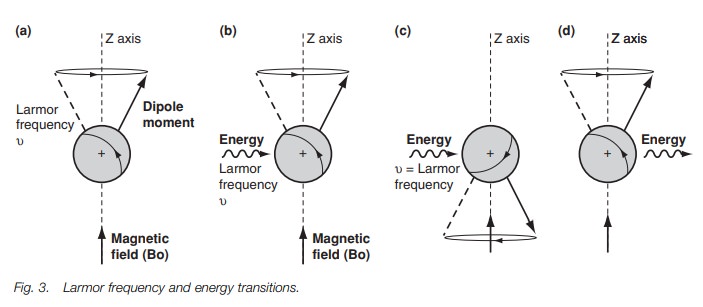
In order to get a spectrum we need to get transitions between the two energy levels. This can be achieved by firing in a burst of energy in the form of electro-magnetic radiation (Fig. 3b). The effect of this energy is to excite the nucleus and to cause it to ‘flip’ such that it is now against the magnetic field (Fig. 3c). This orientation is less stable than the original orientation and so the nucleus has absorbed energy. It is found that the energy required to do this has the same frequency as the Larmor frequency. If the electromagnetic radiation is now stopped, the nucleus relaxes back to the more stable orientation (Fig. 3d). As a result, energy is emitted. Such energy can be detected and measured leading to a signal in an nmr spectrum. The energy difference between the two orientations is extremely small and is in the radiofrequency region of the electromagnetic spectrum. The energy difference is proportional to the Larmor frequency, which is proportional to the strength of the external applied magnetic field. In a magnetic field of 14 100G, the energy difference is 60 × 10⁶ Hz or 60 MHz. In a magnetic field of 23 500G the energy difference is 100 MHz. NMR spectrometers work at a specific magnetic field and thus a specific electromagnetic radiation is required for resonance. The convention is to identify the spectrometers and their spectra by the strength of the electromagnetic radiation used (i.e. 60 MHz or 100 MHz).