Proton nuclear magnetic resonance spectroscopy: Spin-spin coupling

PROTON NUCLEAR MAGNETIC RESONANCE SPECTROSCOPY

Key Notes

Spin-spin coupling

Spin-spin coupling takes place between protons on neighboring carbon atoms if the protons concerned have different chemical shifts. When the protons on one carbon are in resonance, the protons on the neighboring carbon are not and each neighboring proton can adopt two possible orientations. These orientations affect the signal of the proton(s) that are in resonance, resulting in a splitting of the signal. The effect is transmitted through bonds rather than through space and decreases in magnitude with the number of bonds involved, such that coupling does not usually take place beyond three bonds. The number of peaks resulting from splitting is one more than the number of neighboring protons. The size of the splitting is called the coupling constant and this is identical for both signals involved in the coupling.

Spin-spin coupling

So far, we have looked at spectra where each signal is a single peak (singlet).

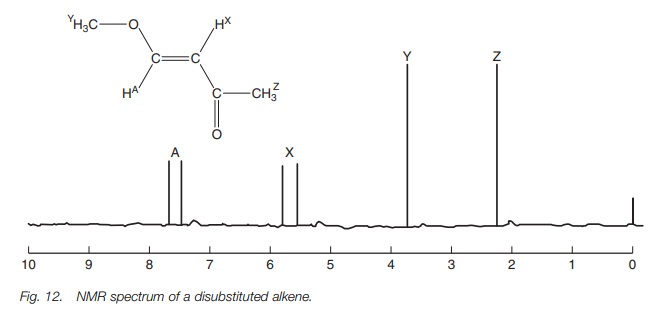
However, in many spectra, the signal for a particular proton is made up of two or more  peaks.  This  is  due  to  an  effect  known  as  spin-spin  coupling  which  is normally seen when non-equivalent protons are on neighboring carbon atoms. An example of this can be seen in the nmr spectrum of the alkene shown in Fig. 12.There are four non-equivalent protons present in this molecule and so we would expect four signals. The spectrum does indeed show four signals although there are six peaks present. The signals at 2.2 ppm and 4.7 ppm are due to the two methyl groups and are both singlets. However, the signals for the two alkene protons are both split into doublets. Thus, the two peaks between 5 and 6 ppm constitute one signal due to H^X. The chemical shift of this signal is the midpoint between the two peaks, i.e. at 5.65 ppm. Similarly the two peaks between 7 and 8 ppm constitute one signal due to H^A, with the chemical shift being the midpoint between the two peaks at 7.6 ppm.

 The alkene signals are present as doublets since the alkene protons A and X are coupling with each other and are mutually influencing the magnetic field that they experience. In Fig. 13, we have a simplified diagram where the two alkene protons are in white, separated from each other by three bonds and the two alkenecarbon atoms in black.

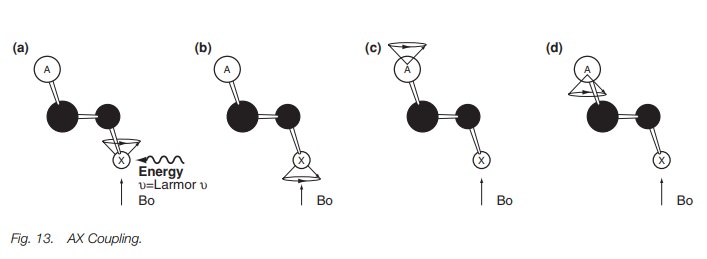
Let us concentrate on proton X in Fig.13a. An external magnetic field Bo forces this proton to adopt two possible orientations with the more stable orientation shown in Fig. 13a. Energy having the same frequency as the Larmor frequency is now applied resulting in resonance and a signal in the nmr spectrum.

So much for proton X, but what is happening to proton A while all this is hap-pening? Applying a magnetic field also forces this proton to adopt two possible orientations (Figs. 13c and d). However, the precessional frequency for proton A is different from that of proton X since proton A is in a different environment. There-fore, applying energy which has the correct frequency to make proton X resonate will have no such effect on proton A. This means that the two possible orientations for proton A are long lived, and resonance does not take place between them. The dipole moments associated with these orientations can thus generate a small magnetic field that will influence X. So essentially proton A can be viewed as a small magnet which has two different orientations. The two different magnetic fields generated by A are experienced by proton X but it is important to realize that the effect is not transmitted through space. The nuclei are too far apart from each other for that to happen. Instead the effect is transmitted through the three bonds between the two protons. A full explanation of how this happens is not possible here but the overall effect is that proton A generates two equal but oppos-ing secondary magnetic fields at proton X. The same thing happens in reverse when energy is applied to resonate proton A. In that situation, proton X does not resonate but has two equal and opposite secondary magnetic effects on A.

Let us look at what happens to the signal for proton A when this coupling takes place (Fig. 14). If coupling did not place, the signal would be a singlet. However with coupling, A experiences two different secondary magnetic fields from X and is split into two peaks.

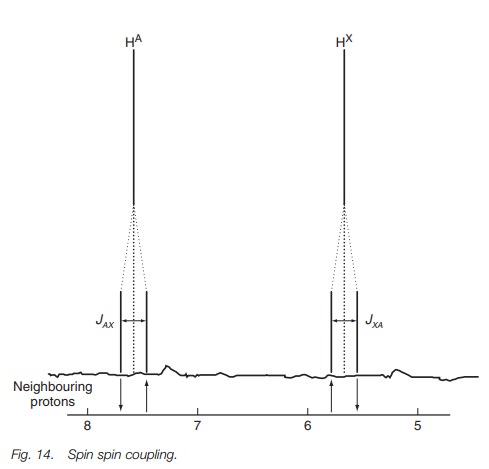
The peak at higher chemical shift occurs when the secondary field generated by proton X is aligned with the applied field. The peak at lower chemical shift occurs when the secondary field is against the applied field. Since both effects are equally likely and of the same magnitude the signal for A is split into a doublet where the peaks are of equal height and equally shifted from the original chemical shift. The separation between the peaks can be measured and is called the coupling con-stant. It is given the symbolJand is measured in hertz rather than ppm. The cou-pling is further specified by defining the coupled protons. Thus, J_AX is the coupling constant between proton A and proton X.

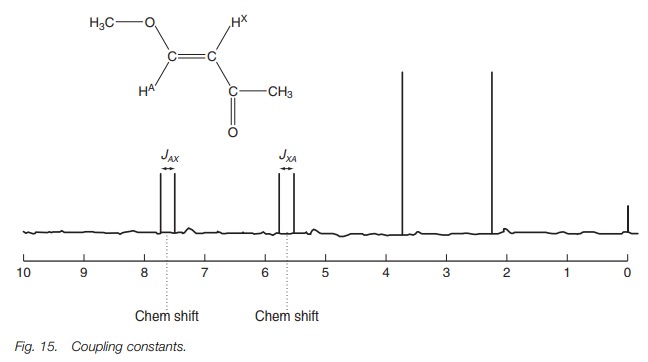
If we look now at the signal for X, the same thing happens except the secondary magnetic fields are now due to the different orientations of proton A. The cou-pling constant for this signal is J_XA and must be equal in magnitude to J_AX (Fig. 15).

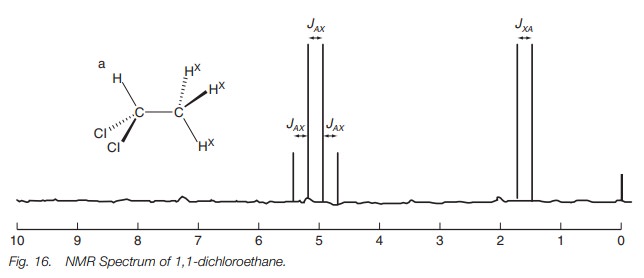
Let us now look at a more complicated situation where we have a methyl group linked to a methine group (see 1,1-dichloroethane; Fig. 16). In this situation, we have three identical methyl protons (X) separated by three bonds from one CH proton (A). The spectrum shows two signals. The signal for the methyl protons is a doublet at 1.55 ppm, while the signal for the methine proton is a quartet at 5.05 ppm.

We look first of all at the effect the methine proton has on the three equivalent methyl protons. The methine proton can have two possible orientations – either with the field or against it. The secondary magnetic field associated with these orientations is transmitted to the methyl protons through the connecting bonds, which means that the methyl protons are influenced by two equal but opposing secondary magnetic fields. The signal for the methyl protons is split into a doublet.

Let us now consider the influence of the methyl protons on the methine proton. There are several possibilities here. The methyl protons could all be opposed to the applied field or they could all be aligned with the field. Another possibility is for two of the protons to be with the field while one is against the field. Note that this sort of arrangement is three times more likely than having all the protons pointing the same way. Finally, two of the protons could be against the field and one could be with the field. Once again the possibility of this kind of arrangement is three times more likely than having all the nuclei pointing the same way. Since there are four different ways of orientating the three methyl protons, the signal for the methine proton is split into four different peaks (a quartet). These peaks will not be of equal intensity as there is more chance of certain orientations than oth-ers. The relative intensities match the statistical probability of the different orien-tations, i.e. 1 : 3 : 3 : 1.

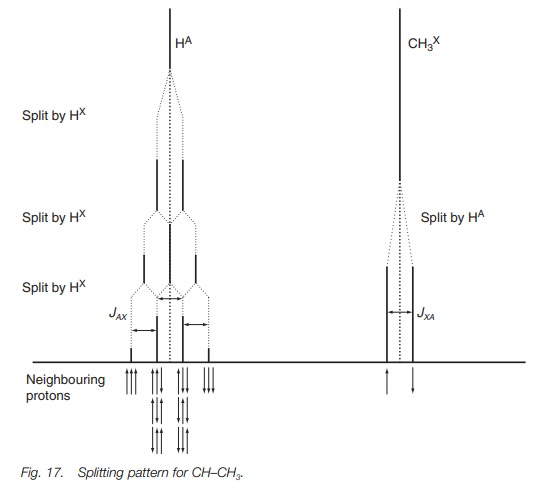
We can predict the number of peaks in the methine signal (A) and their relative intensity in the following manner (Fig. 17). If no coupling took place, the signal would be a singlet. However, there are three neighboring protons due to the methyl group. We shall see what happens when we split the methine signal with each of these methyl protons in turn. Coupling with one of the methyl protons splits the signal into a doublet of intensity 1 : 1. Splitting with a second methyl pro-ton splits each of these peaks into a doublet. Since the splitting is identical, the two inner peaks of each doublet overlap to give a single peak such that we end up with a triplet having an intensity of 1 : 2 : 1. Each of these peaks is now split by the effect of the third methyl proton to give a quartet of ratio 1 : 3 : 3 : 1. The peak at highest chemical shift corresponds to the arrangement where the secondary magnetic field of all three methyl protons is with the applied field and enhancing it. The peak at the next highest chemical shift corresponds to the situation where two of the methyl protons are with the applied field and the third is against it. The next peak has two protons against the applied field and one proton with it. Finally we have the peak at the lowest chemical shift, which corresponds to the situation where the magnetic fields of all three methyl protons oppose the applied field. Note that the chemical shift for the signal is the same as it would have been if no splitting had occurred (i.e. the middle of the signal). The coupling constants J_AX and J_XA are identical for both signals since they are coupled together.

It is possible to rationalize the coupling patterns and peak intensities for other coupling systems in a similar manner, but a quicker method is to use a system known as Pascall’s triangle (Fig. 18). To use the triangle, you first identify the number of protons that are neighboring the group of interest. This defines which row of the triangle is relevant. The row indicates the number of peaks one would expect in the signal and their relative intensity. Consider for example 1,1-dichloroethane (Fig. 16). The methine group has a neighboring methyl group and so there are three neighboring protons. 

The relevant row in Pascall’s triangle has four entries and so the signal for the methine proton is a quartet with a ratio of 1 : 3 : 3 : 1. When we consider the methyl group, it has one neighboring proton and so Pascall’s triangle predicts a doublet of ratio 1 : 1.

Note that the number of peaks in a signal is always one more than the number of neighboring protons.

It is important to note that coupling can only take place between non-equiva-lent protons of different chemical shifts. Coupling between the protons making up a methyl group is not possible since they are equivalent to each other. Similarly, coupling is not possible between the methyl groups of ethane since these groups cannot be distinguished from each other. It is also important to remember that the coupling is transmitted through bonds and that the size of this coupling decreases with the number of bonds involved. In fact, coupling is rarely seen between pro-tons which are separated from each other by more than three bonds. In effect, this means that most coupling takes place between non-equivalent protons on neigh-boring carbon atoms.