Probability Mass Function

Probability mass function and probability density function

A probability function is associated with each value of the random variable. This function is used to compute probabilities for events associated with the random variables. The probability function defined for a discrete random variable is called probability mass function. The probability function associated with continuous random variable is called probability density function.

Probability Mass Function

If, X is a discrete random variable taking values x1, x2  …. xn  with respective probabilities p(x1), p(x2) ….. p(xn) such that

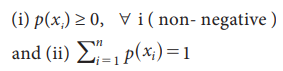
then p(x) is known as the probability mass function (p.m.f) of the discrete random variable X.

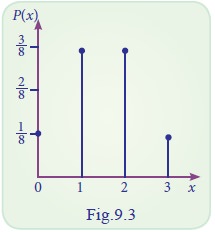
The pair {xi, p(xi); i = 1, 2, 3, ... } is known as prabability distribution of X.

Example 9.8

A coin is tossed two times. If X is the number of heads, find the probability mass function of X.

Solution:

Since the coin is tossed two times, the sample space is S={HH, HT, TH, TT}

If X denotes the numbers of heads, the possible values of X are 0,1,2 with the following

Example 9.9

In example 9.3 the probability mass function of X is given in the following table

The above table may be called as the probability distribution function of X.