Definition of random variable

Definition of random variable

Definition

Let S be the sample space of a random experiment. A rule that assigns a single real number to each outcome (sample point) of the random experiment is called random variable.

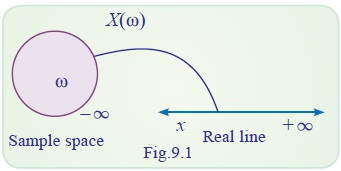
In other words, a random variable is a real valued function defined on a sample space S that is with each outcome ω of a random experiment there corresponds a unique real value x known as a value of the random variable X. That is X(ω ) = x.

Generally random variables are denoted by upper case alphabets like X, Y, Z … and their values or realizations are denoted by the corresponding lower case letters. For example, if X is a random variable, the realizations are x₁, x₂ …

Example 9.1

Consider the random experiment of rolling a die.

The sample space of the experiment is S={1, 2, 3, 4, 5, 6}

Let X denotes the face of the die appears on top.

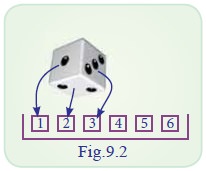
The assigning rule is

X(1) = 1, X(2) = 2, X(3) = 3, X(4)=4, X(5)=5 and X(6)=6

Hence the values taken by the random variable X are 1,2,3,4,5,6. These values are also called the realization of the random variable X.

Example 9.2

Random experiment : Two coins are tossed simultaneously.

Sample space : S={HH, HT, TH, TT}

Assigning rule : Let X be a random variable defined as the number of heads comes up.

Here, the random variable X takes the values 0, 1, 2 .

Example 9.3

Experiment : Two dice are rolled simultaneously.

Sample space : {(1, 1),(1, 2),(1, 3),…(6, 6)}

Assigning rule : Let X denote the sum of the numbers on the faces of dice

then X_ij = i + j, Here, i denotes face number on the first die and j denotes the face number on the second die.

Then X is a random variable which takes the values 2, 3, 4 . .… 12.

That is the range of X is {2, 3, 4…… 12}