Addition and Multiplication Theorem on Expectations

Addition and Multiplication Theorem on Expectations

Addition Theorem on Expectations

1. Statement for Discrete random variable

If X and Y are two discrete random variables then

(X+Y) = E(X) + E(Y)

Proof

Let the random variable X assumes the values x₁, x₂ ... x_n with corresponding probabilities p₁, p₂…..p_n, and the random variable y assume the values y₁, y₂ ……. y_m with corresponding probabilities p₁, p₂…..p_m

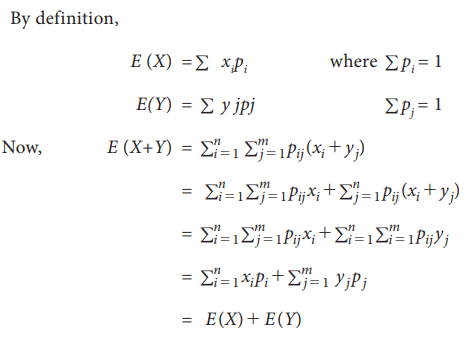
2. Statement for Continuous random variable

Let X and Y are two continuous random variables with probability density functions f(x) and f(y) respectively. Then E (X + Y) = E(X) + E(Y)

Proof:

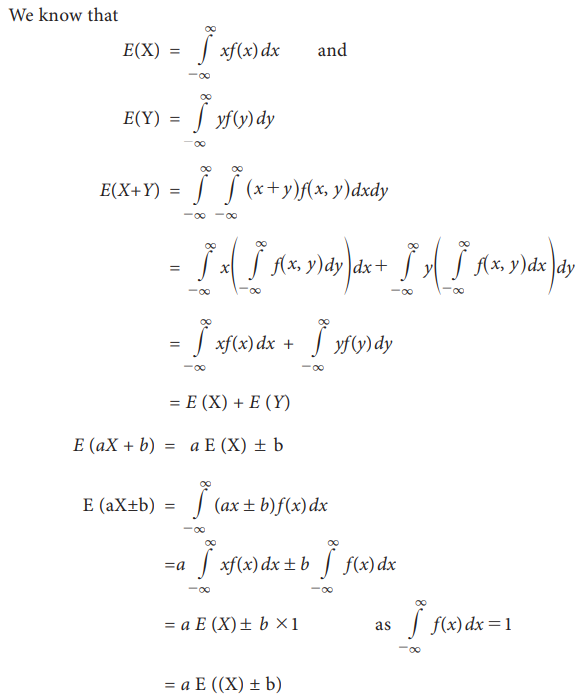
Remarks:

1. Statement: (aX+b) = aE(X)+b where a and b are constants.

Proof: E(aX+b) = E(aX)+E(b) by property 3

= aE(X)+b by property 2

(aX-b) = aE(X)-b

Example 9.23

Find the expectation of the sum of the number obtained on throwing two dice.

Solution:

Let X&Y denote the number obtained on the I and II die respectively. Then each of them is a random variable which takes the value 1,2,3,4,5 and 6 with equal probability 1/6.

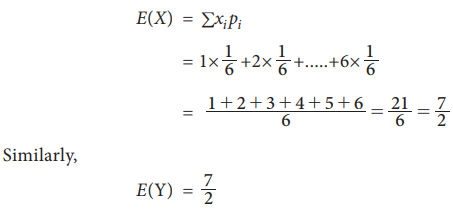
Thus the expectation of the numbers obtained on two dices.

X+Y takes the values 2, 3…12 with their probability given by

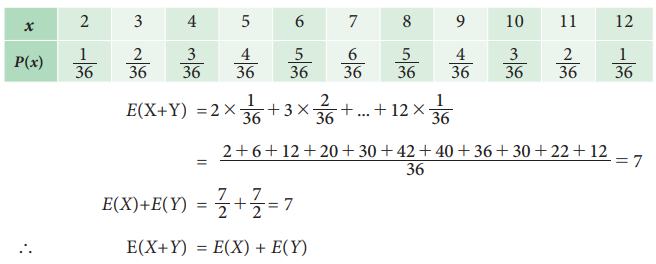
Example 9.24

Let X and Y are two random variables with p.d.f given by

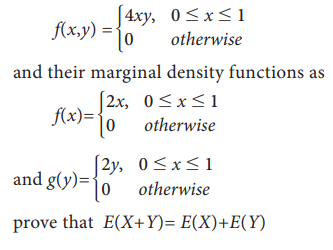
Solution:

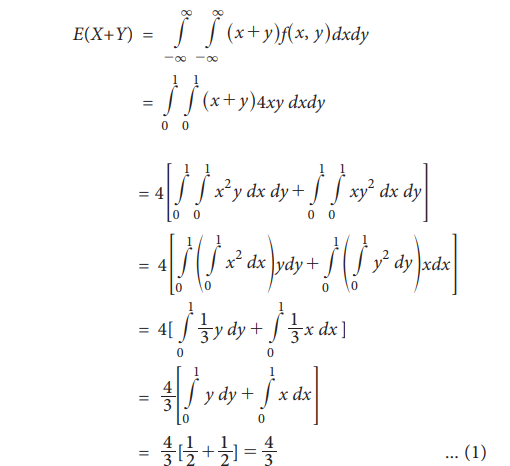
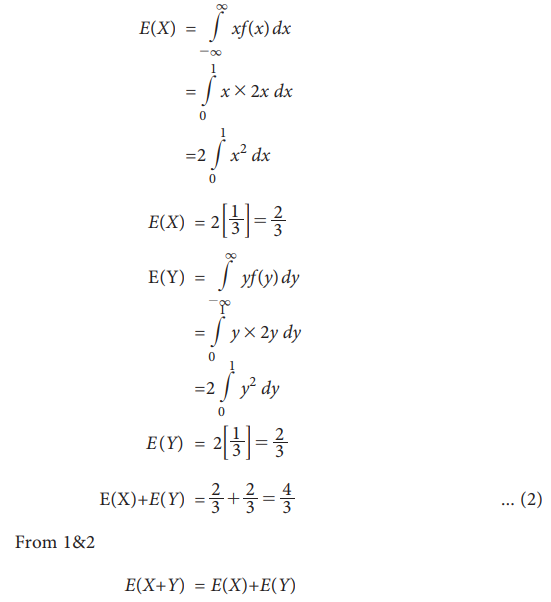
Multiplication Theorem on Expectation

Discrete random variable:

Statement: If X and Y are two independent variables then E(XY) = E (X) E(Y)

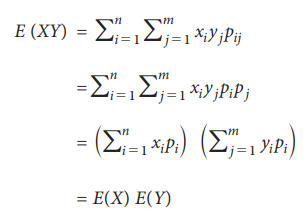
Continuous random variable:

Statement: If X and Y are independent random variables Then E (XY) = E(X) E(Y)

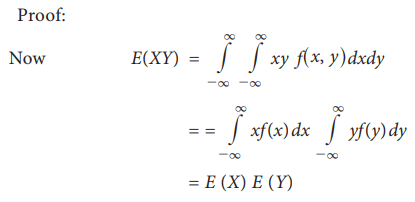
Example 9.25

Two coins are tossed one by one. First throw is considered as X and second throw is considered as Y following joint probability distribution is given by,

[getting Head is taken as 1 and Tail is taken as 0]

Verify E(XY)= E(X) E(Y)

Solution:

A random variable XY can take the values 0 and 1

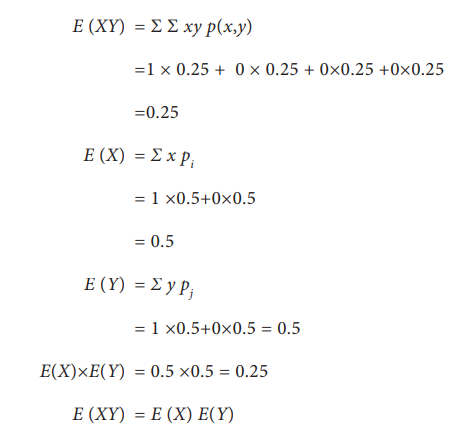
[It is applicable only when X and Y are independent]

Example 9.26

The independent random variables X and Y have the p.d.f given by

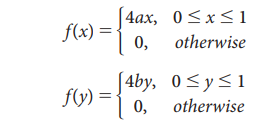
Prove that E(XY) = E(X) E(Y)

Solution:

X and Y are independent

f(x,y) = f(x) × f(y)

f(x,y) = 4ax×4by