Moments

Moments

Another approach helpful to find the summary measures for probability distribution is based on the ‘moments’. We will discuss two types of moments.

i. Moments about the origin. (Origin may be zero or any other constant say A ). It is also called as raw moments.

ii. Moments about the mean is called as central moments.

Moments about the origin

First order central moment:

put r = 1 in the definition, 

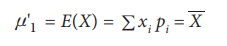
This is called the mean of the random variable X. Hence the first order raw moment is mean.

Second order raw moment

Put r = 2 then

μ'₂ = E(X²)= Σx_i²p_i

This is called second order raw moment about the origin.

Moments about the origin

First order central moment:

put r = 1 in the definition,

This is called the 2^nd central moment about the mean and is known as the variance of the random variable X.

i.e., Variance = Var (X) =μ₂ = μ₂' - (μ₁')²

Standard Deviation (S.D) = σ = √variance

Some results based on variance:

i. Var (c) = 0 i.e. Variance of a constant is zero

ii. If c is constant then Var (cX)=c² Var(X)

iii. If X is a random variable and c is a constant then Var (X ± c) = Var (X)

iv. a and b are constants then Var (aX ± b) = a² Var (X)

v. a and b are constants then Var (a ± bX) = b² Var (X).

vi. If X and Y are independent random variables then Var (X + Y) = Var (X) + Var(Y)

Moment generating function(M.G.F.)

Definition:

A moment generating function (m.g.f) of a random variable X about the origin is denoted by M_x(t) and is given by

M_x(t) = E (e^tx) , |t| <1

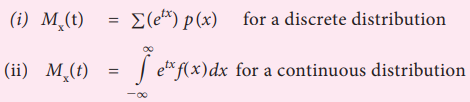
From the series on the right hand side, μ_r’ is the coefficient of r^t/r! in Mx (t) .

For a random variable X to find the moment about origin we use moment generating function.

Since M_x (t) generates moments of the distribution and hence it is known as moment generating function.

Using the function, we can find mean and variance by using the first two raw moments.

 μ₂= μ₂’-( μ₁’)²

Characteristic function

For some distribution, the M.G.F does not exist. In such cases we can use the characteristic function and it is more servicable function than the M.G.F.