Chapter: 11th Statistics : Chapter 9 : Random Variables and Mathematical Expectation
Joint and marginal probability mass functions
Joint
and marginal probability mass functions
In
real life situations we may be observed two or more random variables on the
individuals simultaneously. For instance, blood pressure and cholesterol for
each individual are measured simultaneously. In such cases we require the
concept of bi-variate random variable represented by ( X,
Y ), where X and Y are univariate random variables.
Definition (Joint p.m.f)
Let
(X, Y) be a discrete bivariate random
variable. Then p (x, y) is called the joint probability
mass function of (X, Y) if the following conditions are
satisfied.
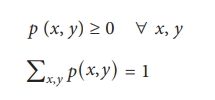
Definition (Marginal Probability Mass Function)
Given a
joint probability mass function p (x, y), then p (x) = Σy p(x,y) is
called marginal probability mass function of X. Similarly p (y) = Σx p(x,y) is
called the marginal probability mass function of Y.
Example 9.14
There
are 10 tickets in a bag which are numbered 1, 2, 3, ...10. Two tickets are
drawn at random one after the other with replacement.
Here, random variable X
denotes the number on the first ticket and random variable Y denotes the number on the second ticket.
Joint and marginal probability density functions
As we defined in section 9.5.1 the joint probability mass
function, we define the joint probability density function.
Definition:
Let (X, Y) be a bivariate
continuous random variables. The function f
(x, y) is called a bivariate probability density if the following conditions
are satisfied.
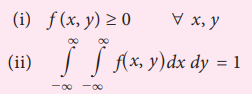
The marginal probability density function of X is given by
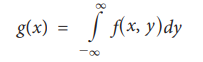
and the marginal probability density function of Y is given by

Example 9.15
Prove that the bivariate function given by f(x, y) = 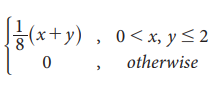
Proof:
If f is a probability density function
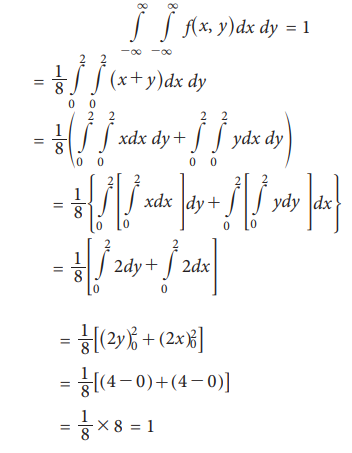
Therefore,
f (x, y) is a probability density
function.
Example 9.16
Joint
p.d.f. of X,Y is f(x, y) = 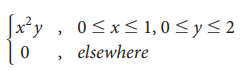 then find the
marginal density function of X and Y.
then find the
marginal density function of X and Y.
Solution:

Example 9.17
Joint
p.d.f. of X,Y is f(x, y) = 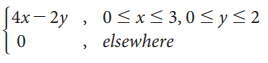 Find the
marginal density function of X and Y
Find the
marginal density function of X and Y
Solution:
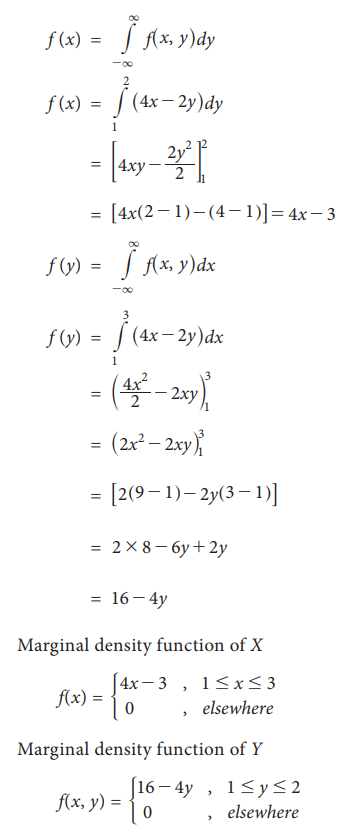
Related Topics