Mathematical expectation

Mathematical expectation

Probability distribution gives us an idea about the likely value of a random variable and the probability of the various events related to random variable. Even though it is necessary for us to explain probabilities using central tendencies, dispersion, symmetry and kurtosis. These are called descriptive measures and summary measures. Like frequency distribution we have to see the properties of probability distribution. This section focuses on how to calculate these summary measures. These measures can be calculated using

i. Mathematical Expectation and variance.

ii. Moment Generating Function .

iii. Characteristic Function.

Expectation of Discrete random variable

Let X be a discrete random variable which takes the values x₁, x₂  ….. x_n  with respective probabilities p₁, p₂ ….. p_n then mathematical expectation of X denoted by E(X)is defined by

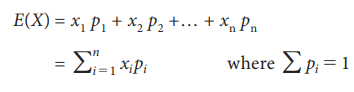
Sometimes E(X) is known as the mean of the random vairable X.

Result:

If g(X) is a function of the random variable X, then E g(X) = Σg(x)p(X = x)

Properties:

E(c) = c where c is a constant

Proof:

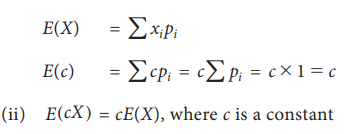
Proof:

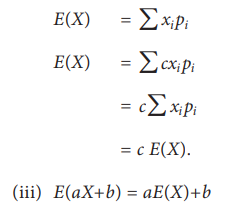
Variance of Discrete random variable

Definition: In a probability distribution Variance is the average of sum of squares of deviations from the mean. The variance of the random variable X can be defined as.

Var ( X ) = E (X – E(X))²

= E (X² ) – ( E(X))²

Example 9.18

When a die is thrown X denotes the number turns up. Find E(X), E(X²) and Var(X).

Solution:

Let X denoted that number turns up in a die.

X takes the values 1, 2, 3, 4, 5, 6 with probabilities 1/6 for each.

Therefore the probability distribution is

Example 9.19

The mean and standard deviation of a random variable X are 5 and 4 respectively Find E (X²)

Solution:

Given E (X) = 5 and σ = 4

` Var (X) = 16

But, Var (X) = E(X²) – [E(X)]²

16 = E (X²) – (5)²

E(X²) = 25 + 16 = 41

Example 9.20

A player tosses two coins, if two head appears he wins ` 4, if one head appears he wins ` 2, but if two tails appears he loses ` 3. Find the expected sum of money he wins?

Solution:

Let X be the random variable denoted the amount he wins.

The possible values of X are 4, 2 and –3

Example 9.21

Let X be a discrete random variable with the following probability distribution

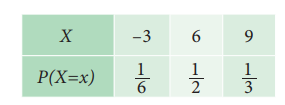
Find mean and variance

Solution: 

Mean = E(X) = ∑x_i p_i

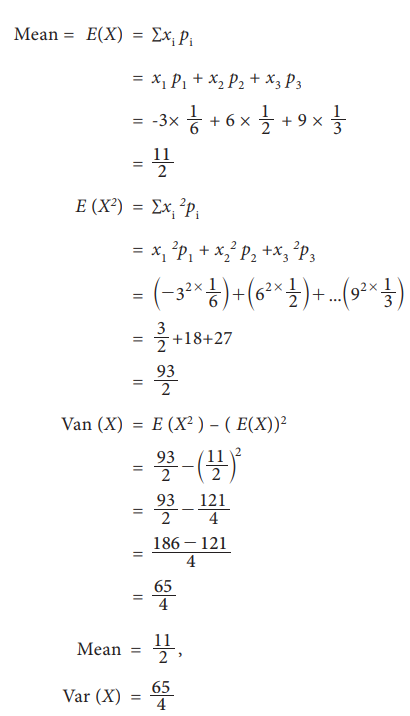
Expectation of a continuous random variable

Let X be a continuous random variable with probability density function f (x) then the mathematical expectation of X is defined as

Results:

E(c) = c where c is constant

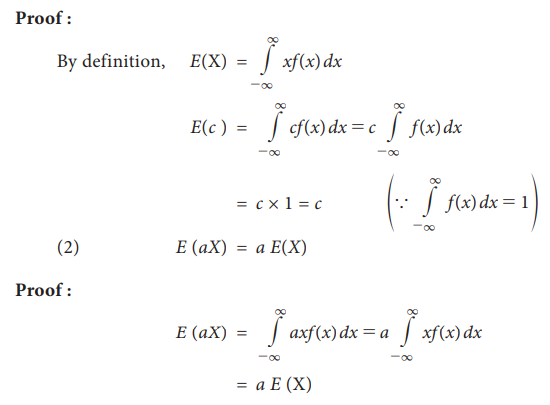
Example 9.22

The p.d.f. of a continuous random variable X is given by

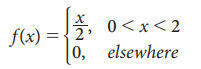
find its mean and variance 

Solution:

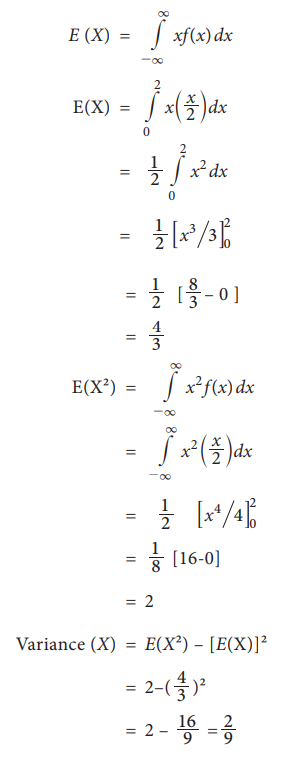
So far we have studied how to find mean and variance in the case of single random variables taken at a time but in some cases we need to calculate the expectation for a linear combination of random variables like aX + bY or the product of the random variables cX × dY or involving more number of random variables. So here we see theorems useful in such situations.

Independent random variables

Random variables X and Y are said to be independent if the joint probability density function of X and Y can be written as the product of marginal densities of X and Y.

That is f (x,y)= g(x) h(y)

Here g(x) marginal p.d.f. of X

h(y) marginal p.d.f. of Y